题目内容
14．平面向量$\overrightarrow{a}$=（1，-2），$\overrightarrow{b}$=（2，m-1），$\overrightarrow{c}$=（4，n），若$\overrightarrow{a}$∥$\overrightarrow{b}$，$\overrightarrow{b}$⊥$\overrightarrow{c}$，则m+n的值为（ ）| A． | 1 | B． | -1 | C． | 2 | D． | -2 |
分析 根据向量的平行和垂直关系，求出m，n的值即可．
解答 解：$\overrightarrow{a}$=（1，-2），$\overrightarrow{b}$=（2，m-1），$\overrightarrow{c}$=（4，n），
若$\overrightarrow{a}$∥$\overrightarrow{b}$，$\overrightarrow{b}$⊥$\overrightarrow{c}$，
则m-1=-4，8+n（m-1）=0，
解得：m=-3，n=2，
则m+n=-1，
故选：B．
点评 本题考查了向量的平行、垂直关系，考查向量的运算，是一道基础题．
练习册系列答案
课时训练江苏人民出版社系列答案
黄冈经典趣味课堂系列答案
启东小题作业本系列答案
相关题目
5．直线y+2=k （x+1）恒过点（ ）
| A． | （2，1） | B． | （-2，-1） | C． | （-1，-2） | D． | （1，2） |
2．
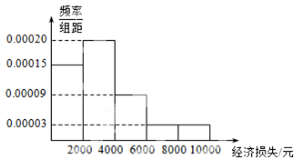适逢暑假，小王在某小区调查了50户居民由于洪灾造成的经济损失，将收集的数据分成[0，2000]，（2000，4000]，（4000，6000]，（6000，8000]，（8000，10000]五组，并作出频率分布直方图（如图）．
（Ⅰ）小王向班级同学发出为该小区居民捐款的倡议．若先从损失超过6000元的居民中随机抽出2户进行捐款援助，求这2户不在同一分组的概率；
（Ⅱ）洪灾过后小区居委会号召小区居民为洪灾重灾区捐款，小王调查的50户居民的捐款情况如表，在表格空白处填写正确的数字，并说明是否有95%以上的把握认为捐款数额多于或少于500元和自身经济损失是否到4000元有关？
参考公式：K2=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$（其中n=a+b+c+d为样本容量）．
适逢暑假，小王在某小区调查了50户居民由于洪灾造成的经济损失，将收集的数据分成[0，2000]，（2000，4000]，（4000，6000]，（6000，8000]，（8000，10000]五组，并作出频率分布直方图（如图）．（Ⅰ）小王向班级同学发出为该小区居民捐款的倡议．若先从损失超过6000元的居民中随机抽出2户进行捐款援助，求这2户不在同一分组的概率；
（Ⅱ）洪灾过后小区居委会号召小区居民为洪灾重灾区捐款，小王调查的50户居民的捐款情况如表，在表格空白处填写正确的数字，并说明是否有95%以上的把握认为捐款数额多于或少于500元和自身经济损失是否到4000元有关？
| 经济损失不超过4000元 | 经济损失超过4000元 | 合计 | |
| 捐款超过500元 | 30 | 9 | 39 |
| 捐款不超过500元 | 5 | 6 | 11 |
| 合计 | 35 | 15 | 50 |
| P（K2≥k0） | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
9．中国古代数学名著《张丘建算经》中记载：“今有马行转迟，次日减半，疾七日，行七百里．”意思是：现有一匹马行走的速度逐渐减慢，每天走的里程数是前一天的一半，连续行走7日，共走了700里．若该匹马连续按此规律行走，则它在第8天到第14天这7天时间所走的总里程为（ ）
| A． | 350里 | B． | 1050里 | C． | $\frac{175}{32}$里 | D． | .$\frac{22575}{32}$里 |
如图所示的三角形数阵角“莱布尼兹调和三角形”，它是由整数的倒数组成的，第n行有n个数，且两端的数均为$\frac{1}{n}（{n≥2}）$，每个数使它下一行左右相邻两个数的和，如$\frac{1}{1}=\frac{1}{2}+\frac{1}{2}，\frac{1}{2}=\frac{1}{3}+\frac{1}{6}，\frac{1}{3}=\frac{1}{4}+\frac{1}{12}$，则第7行第5个数（从左到右）为$\frac{1}{105}$．
3．在△ABC中，AB=3，AC=2，BC=$\sqrt{10}$，则$\overrightarrow{AC}$•$\overrightarrow{AB}$=（ ）
| A． | $\frac{2}{3}$ | B． | $-\frac{2}{3}$ | C． | $\frac{3}{2}$ | D． | $-\frac{3}{2}$ |