题目内容
以平面直角坐标系的原点为极点,x轴的非负半轴为极轴建立极坐标系,使极坐标系的单位长度与直角坐标系的单位长度相同.已知直线l的参数方程为
(t为参数),曲线C的极坐标方程为ρ=4cosθ,则直线l与曲线C的交点个数为 .
|
考点:参数方程化成普通方程
专题:坐标系和参数方程
分析:应用代入法,将参数方程化为普通方程,应用x=ρcosθ,y=ρsinθ,ρ2=x2+y2将极坐标方程化为普通方程,联立两方程消去y,得到x的二次方程,通过方程的根的情况即可得到交点个数.
解答:
解:直线l的参数方程为
(t为参数),可化为普通方程为:y=
(x+2),
曲线C的极坐标方程为ρ=4cosθ,可化为直角坐标方程为:x2+y2-4x=0,
将直线方程代入得,
x2+
x-4x+
=0,即x2-2x+1=0,
解得x1=x2=1,故交点个数为1.
故答案为:1.
|
| ||
| 3 |
曲线C的极坐标方程为ρ=4cosθ,可化为直角坐标方程为:x2+y2-4x=0,
将直线方程代入得,
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
解得x1=x2=1,故交点个数为1.
故答案为:1.
点评:本题主要考查参数方程化为普通方程,极坐标方程化为普通方程,考查直线方程和曲线方程联立,消去一个变量,应用二次方程的解来判断交点个数.

练习册系列答案
 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
若圆(x-3)2+(y+5)2=r2上的点到直线4x-3y-2=0的最近距离等于1,则半径r的值为( )
| A、4 | B、5 | C、6 | D、9 |
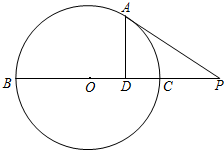 如图所示,PA与圆O相切于A,直线PO交圆O于B,C两点,AD⊥BC,垂足为D,且D是OC的中点,若PA=6,则PC=
如图所示,PA与圆O相切于A,直线PO交圆O于B,C两点,AD⊥BC,垂足为D,且D是OC的中点,若PA=6,则PC=