题目内容
4.已知f(x)=$\frac{x}{x+1}$,x≥0,若f1(x)=f(x),fn+1(x)=f(fn(x)),n∈N+,则f2016(x)的表达式为${f_{2016}}(x)=\frac{x}{1+2016x}$.分析 由题意,可先求出f1(x),f2(x),f3(x)…,归纳出fn(x)的表达式,即可得出f2016(x)的表达式.
解答 解:由题意f1(x)=f(x)=$\frac{x}{x+1}$,
f2(x)=f(f1(x))=$\frac{\frac{x}{x+1}}{1+\frac{x}{x+1}}=\frac{x}{1+2x}$,
f3(x)=f(f2(x))=$\frac{\frac{x}{2x+1}}{1+\frac{x}{2x+1}}=\frac{x}{1+3x}$,
…
fn(x)=f(fn-1(x))=$\frac{x}{1+nx}$,
归纳法得:${f_{2016}}(x)=\frac{x}{1+2016x}$.
故答案为:${f_{2016}}(x)=\frac{x}{1+2016x}$.
点评 本题考查逻辑推理中归纳推理,由特殊到一般进行归纳得出结论是此类推理方法的重要特征,是基础题.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案
相关题目
16.已知13+23+33+…+n3=$\frac{{{n^2}{{(an+b)}^2}}}{4}$对一切n∈N+都成立,那么a,b的可能值为( )
| A. | a=b=1 | B. | a=1,b=2 | C. | a=2,b=1 | D. | 不存在这样的a,b |
13.为减少“舌尖上的浪费”,我校的学生会干部对一中,城关中学的食堂用餐的学生能否做到“光盘”进行调查.现从中随机抽取男、女生各25名进行问卷调查,得到了如下列联表:
(Ⅰ)补全相应的2×2列联表;
(Ⅱ)运用独立性检验的思想方法分析:能否在犯错误的概率不超过0.05的前提下认为在学校食堂用餐的学生能做到“光盘”与性别有关?并说明理由.
| 男性 | 女性 | 合计 | |
| 做不到“光盘” | 18 | ||
| 能做到“光盘” | 14 | ||
| 合 计 | 50 |
(Ⅱ)运用独立性检验的思想方法分析:能否在犯错误的概率不超过0.05的前提下认为在学校食堂用餐的学生能做到“光盘”与性别有关?并说明理由.
14.黑白两种颜色的正六边形地面砖按如图的规律拼成若干个图案,则第2016个图案中的白色地面砖有( )
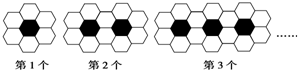

| A. | 8064块 | B. | 8066块 | C. | 8068块 | D. | 8070块 |
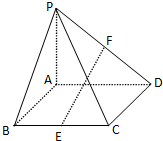 如图,在四棱锥P-ABCD中,底面ABCD为矩形,侧棱PA⊥底面ABCD,点E,F分别为BC、PD的中点,若PA=AD=4,AB=2.
如图,在四棱锥P-ABCD中,底面ABCD为矩形,侧棱PA⊥底面ABCD,点E,F分别为BC、PD的中点,若PA=AD=4,AB=2.