题目内容
14.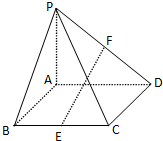 如图,在四棱锥P-ABCD中,底面ABCD为矩形,侧棱PA⊥底面ABCD,点E,F分别为BC、PD的中点,若PA=AD=4,AB=2.
如图,在四棱锥P-ABCD中,底面ABCD为矩形,侧棱PA⊥底面ABCD,点E,F分别为BC、PD的中点,若PA=AD=4,AB=2.(1)求证:EF∥平面PAB.
(2)求直线EF与平面PCD所成的角.
分析 (1)以A为原点,分别以AB、AD、AP所在直线为x轴、y轴、z轴,建立空间直角坐标系,$\overrightarrow{EF}$=(-2,0,2),平面PAB的一个法向量是$\overrightarrow{AD}$=(0,4,0),证明$\overrightarrow{EF}⊥\overrightarrow{AD}$,即可证明EF∥平面PAB;
(2)求出平面PCD的一个法向量,即可求直线EF与平面PCD所成的角.
解答 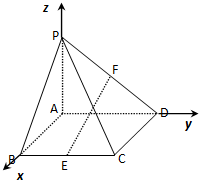 (1)证明:依题意,以A为原点,分别以AB、AD、AP所在
(1)证明:依题意,以A为原点,分别以AB、AD、AP所在
直线为x轴、y轴、z轴,建立空间直角坐标系如图,则A(0,0,0),B(2,0,0),P(0,0,4),D(0,4,0)C(2,4,0),E(2,2,0),F(0,2,2)------------------(2分)
∴$\overrightarrow{EF}$=(-2,0,2),平面PAB的一个法向量是$\overrightarrow{AD}$=(0,4,0)------(4分)
∵$\overrightarrow{EF}•\overrightarrow{AD}$=0,
∴$\overrightarrow{EF}⊥\overrightarrow{AD}$,
故 EF∥平面PAB-----------------------------------------------(6分)
(2)∵$\overrightarrow{DC}$=(2,0,0),$\overrightarrow{DP}$=(0,-4,4)(7分)
设平面PCD的一个法向量为$\overrightarrow{m}$=(x,y,z)
则$\left\{\begin{array}{l}{2x=0}\\{-4y+4z=0}\end{array}\right.$得$\left\{\begin{array}{l}x=0\\ y=z\end{array}\right.$∴令z=1,得$\overrightarrow{m}$=(0,1,1)-----------------------------------(9分)
而$\overrightarrow{EF}$=(-2,0,2),
∴cos<$\overrightarrow{EF}$,$\overrightarrow{m}$>=$\frac{0+0+2}{\sqrt{4+4}•\sqrt{1+1}}$=$\frac{1}{2}$,
∴<$\overrightarrow{EF}$,$\overrightarrow{m}$>=60°----------------------------------(11分)
所以EF与平面PCD所成的角是90°-60°=30°----------------------------(12分)
点评 本题考查线面平行的证明,考查线面角,考查向量知识的运用,考查学生分析解决问题的能力,属于中档题.

 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | 1 |
 如图,平面ABCD⊥平面ABE,其中ABCD为矩形,△ABE为直角三角形,∠AEB=90°,AB=2AD=2AE=2.
如图,平面ABCD⊥平面ABE,其中ABCD为矩形,△ABE为直角三角形,∠AEB=90°,AB=2AD=2AE=2.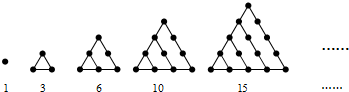
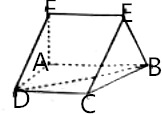 如图,在直角梯形ABCD中,AB∥CD,∠DAB=90°,AD=CD=$\frac{1}{2}$AB=1,直角梯形ABEF可以通过直角梯形ABCD以直线AB为轴旋转得到,且平面ABEF⊥平面ABCD
如图,在直角梯形ABCD中,AB∥CD,∠DAB=90°,AD=CD=$\frac{1}{2}$AB=1,直角梯形ABEF可以通过直角梯形ABCD以直线AB为轴旋转得到,且平面ABEF⊥平面ABCD