题目内容
15.已知圆C:(x-a)2+(y-2)2=4(a∈R)及直线l:x-y+3=0.当直线l被圆C截得的弦长为2$\sqrt{3}$时,求a的值.分析 利用弦长公式可得弦心距d=1,再由点到直线的距离公式可得d=$\frac{|a-2+3|}{\sqrt{2}}$,由此求得a的值.
解答 解:由题意圆C:(x-a)2+(y-2)2=4的圆心坐标是(a,2),半径是2.
利用弦长公式可得弦心距d=$\sqrt{4-3}$=1,
再由点到直线的距离公式可得d=$\frac{|a-2+3|}{\sqrt{2}}$,
∴1=$\frac{|a-2+3|}{\sqrt{2}}$,解得a=-1$±\sqrt{2}$.
点评 本题主要考查直线和圆相交的性质,点到直线的距离公式、弦长公式的应用,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
6.过抛物线y=x2的焦点F作一直线交抛物线于M(x1,y1)、N(x2,y2)两点,如果y1+y2=1,则线段MN的中点到准线的距离等于( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | 1 |
20.已知定义在R上的可导函数f(x)图象既关于直线x=1对称,又关于直线x=5对称,且当x∈[1,5]时,有f′(x)>3f(x),则下列各式成立的是( )
| A. | e3f(-14)<f(-5),e3f(-10)<f(-19) | B. | e3f(-14)>f(-5),e3f(-10)>f(-19) | ||
| C. | e3f(-14)<f(-5),e3f(-10)>f(-19) | D. | e3f(-14)>f(-4),e3f(-10)<f(-19) |
7.已知函数f(x)=-$\frac{1}{3}$x3+x2+ax+b在x=3取得极值为4,则f(x)在区间[-2,1]上的最大值为( )
| A. | -1 | B. | 0 | C. | -$\frac{4}{3}$ | D. | -$\frac{13}{3}$ |
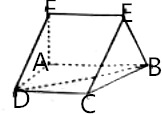 如图,在直角梯形ABCD中,AB∥CD,∠DAB=90°,AD=CD=$\frac{1}{2}$AB=1,直角梯形ABEF可以通过直角梯形ABCD以直线AB为轴旋转得到,且平面ABEF⊥平面ABCD
如图,在直角梯形ABCD中,AB∥CD,∠DAB=90°,AD=CD=$\frac{1}{2}$AB=1,直角梯形ABEF可以通过直角梯形ABCD以直线AB为轴旋转得到,且平面ABEF⊥平面ABCD