题目内容
已知函数f(x)=lnax+bx+
(a、b为常数),在x=-1时取得极值.
(1)求实数b的取值范围;
(2)当a=-1时,关于x的方程f(x)=2x+m有两个不相等的实数根,求实数m的取值范围;
(3)数列{an}满足an=1-
(n∈N*且n≥2),a1=
,数列{an}的前n项和为Sn,求证:2n•an≥eSn+an-1(n∈N*,e是自然对数的底).
| a |
| x |
(1)求实数b的取值范围;
(2)当a=-1时,关于x的方程f(x)=2x+m有两个不相等的实数根,求实数m的取值范围;
(3)数列{an}满足an=1-
| 1 |
| an-1+1 |
| 1 |
| 2 |
考点:导数在最大值、最小值问题中的应用,数列与不等式的综合
专题:导数的综合应用
分析:(1)注意到题目中f(x)在x=-1有定义,初步判断a<0;另外,根据f′(-1)=0且-1是其极值点,列出等式,用b表示a代入计算;
(2)结合着定义域,原题可转化成方程ln(-x)-
=2x+m在(-∞,0)上有两个不等实根.令-x=t,则问题又进一步转化为方程lnt+
+2t=m在(0,+∞)上有两个不等实根,再通过求导的方法对函数g(x)=lnx+
+2x进一步研究.
(3)首先由数列的递推关系式求出数列{an}的通项公式,再利用(2)中的结论,即g(x)=lnx+
+2x≥3-ln2,其中,令x=
,代入不等式,进行化简计算,累加,即可证明原不等式.
(2)结合着定义域,原题可转化成方程ln(-x)-
| 1 |
| x |
| 1 |
| t |
| 1 |
| x |
(3)首先由数列的递推关系式求出数列{an}的通项公式,再利用(2)中的结论,即g(x)=lnx+
| 1 |
| x |
| n |
| n+1 |
解答:
解:(1)f′(x)=
+b-
=
,
∵f(x)在x=-1有定义∴a<0.
由题意知,x=-1是方程
=0的根,且不是重根.
∴b=a+1且1+4ab≠0,
又∵a<0,∴b<1且b≠
;
(2)a=-1时 b=a+1=0即方程ln(-x)-
=2x+m在(-∞,0)上有两个不等实根.
即方程lnx+
+2x=m在(0,+∞)上有两个不等实根.
令g(x)=lnx+
+2x(x>0)g′(x)=
-
+2=
(x>0)
∴g(x)在(0,
]上单调递减,在[
,+∞)上单调递增,
∴当x=
时,g(x)min=g(
)=3-ln2.
又当x→0时,g(x)→+∞;当x→+∞时,g(x)→+∞,
∴当m>3-ln2时,方程f(x)=2x+m有两个不相等的实数根.
(3)an=1-
,∴an=
,
=1+
,
∴{
}是以2为首项,1为公差的等差数列.
∴
=n+1.
∴an=
.
由(2)知g(x)=lnx+
+2x≥3-ln2,
令x=
得:ln
+
+
≥3-ln2,即ln
+ln2≥
-
,
∴ln
+ln2≥
-
,ln
+ln2≥
-
,
…,
ln
+ln2≥
-
,
累加得,ln
+nln2≥
+
+…+
+
-1=Sn+an-1,
即lnan+ln2n≥Sn+an-1
∴an•2n≥eSn+an-1.
| 1 |
| x |
| a |
| x2 |
| bx2+x-a |
| x2 |
∵f(x)在x=-1有定义∴a<0.
由题意知,x=-1是方程
| bx2+x-a |
| x2 |
∴b=a+1且1+4ab≠0,
又∵a<0,∴b<1且b≠
| 1 |
| 2 |
(2)a=-1时 b=a+1=0即方程ln(-x)-
| 1 |
| x |
即方程lnx+
| 1 |
| x |
令g(x)=lnx+
| 1 |
| x |
| 1 |
| x |
| 1 |
| x2 |
| 2x2+x-1 |
| x2 |
∴g(x)在(0,
| 1 |
| 2 |
| 1 |
| 2 |
∴当x=
| 1 |
| 2 |
| 1 |
| 2 |
又当x→0时,g(x)→+∞;当x→+∞时,g(x)→+∞,
∴当m>3-ln2时,方程f(x)=2x+m有两个不相等的实数根.
(3)an=1-
| 1 |
| an-1+1 |
| an-1 |
| an-1+1 |
| 1 |
| an |
| 1 |
| an-1 |
∴{
| 1 |
| an |
∴
| 1 |
| an |
∴an=
| 1 |
| n+1 |
由(2)知g(x)=lnx+
| 1 |
| x |
令x=
| n |
| n+1 |
| n |
| n+1 |
| n+1 |
| n |
| 2n |
| n+1 |
| n |
| n+1 |
| 2 |
| n+1 |
| 1 |
| n |
∴ln
| 1 |
| 2 |
| 2 |
| 2 |
| 1 |
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 2 |
…,
ln
| n |
| n+1 |
| 2 |
| n+1 |
| 1 |
| n |
累加得,ln
| 1 |
| n+1 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n+1 |
| 1 |
| n+1 |
即lnan+ln2n≥Sn+an-1
∴an•2n≥eSn+an-1.
点评:本题是学生容易做错的类型特别是第一小问中的a<0和1+4ab≠0,往往是他们最容易忽视的范围,第二问依旧是在第一问的基础上,将问题转化成我们更为熟悉的内容;最后一问更是综合性比较强,应该说是数列和不等式的综合应用,难度较大,特别是将(2)中的结论应用于该数列,对x的赋值,比较困难,包括后面的化简,也是需要比较高的观察分析能力和计算能力.

练习册系列答案
相关题目
y=f(x)是定义在R上的函数,若a∈R,则“x≠a”是“f(x)≠f(a)”成立的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |

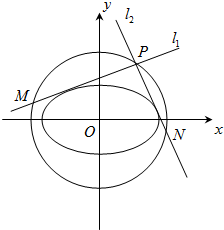 给定椭圆C:
给定椭圆C: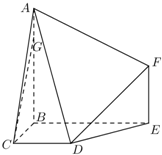 如图,多面体ABCDEF中,BA,BC,BE两两垂直,且AB∥EF,CD∥BE,AB=BE=2,BC=CD=EF=1.
如图,多面体ABCDEF中,BA,BC,BE两两垂直,且AB∥EF,CD∥BE,AB=BE=2,BC=CD=EF=1.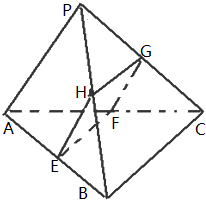 如图,已知点P是三角形ABC所在平面外一点,且PA=BC=1,截面EFGH分别平行于PA,BC(点E,F,G,H分在棱AB,AC,PC,PB上)
如图,已知点P是三角形ABC所在平面外一点,且PA=BC=1,截面EFGH分别平行于PA,BC(点E,F,G,H分在棱AB,AC,PC,PB上)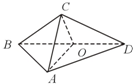 在三棱锥C-ABD中(如图),△ABD与△CBD是全等的等腰直角三角形,O为斜边BD的中点,AB=4,二面角A-BD-C的大小为60°,并给出下面结论:
在三棱锥C-ABD中(如图),△ABD与△CBD是全等的等腰直角三角形,O为斜边BD的中点,AB=4,二面角A-BD-C的大小为60°,并给出下面结论: