题目内容
已知a,b是正数,且ab=a+b+3,则ab的最小值为 .
考点:基本不等式
专题:不等式的解法及应用
分析:由条件利用基本不等式可得ab-2
-3=(
-3)(
+1)≥0,由此求得
的最小值,可得ab的最小值.
| ab |
| ab |
| ab |
| ab |
解答:
解:∵a,b是正数,且ab=a+b+3≥2
+3,
∴ab-2
-3=(
-3)(
+1)≥0,
∴
≥3,
∴ab≥9,故ab的最小值为9,
故答案为:9.
| ab |
∴ab-2
| ab |
| ab |
| ab |
∴
| ab |
∴ab≥9,故ab的最小值为9,
故答案为:9.
点评:本题主要考查基本不等式、一元二次不等式的解法,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知△ABC的周长为
+1,且sinA+sinB=
sinC.若△ABC的面积为
sinC,则角C的大小为( )
| 2 |
| 2 |
| 1 |
| 6 |
| A、30° | B、60° |
| C、90° | D、120° |
设l、m是两条不同的直线,α、β是两个不同的平面,则下列正确的是( )
| A、若l⊥α,l⊥β,则α∥β |
| B、若l∥α,α⊥β,则l⊥β |
| C、若l∥m,m∥α,则l∥α |
| D、若α⊥β,α∩β=l,l⊥m,则m⊥α |
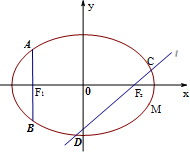 已知椭圆E:
已知椭圆E: