题目内容
 如图,圆锥SO中,AB、CD为底面圆的两条直径,AB交CD于O,且AB⊥CD,SO=OB=2,P为SB的中点.
如图,圆锥SO中,AB、CD为底面圆的两条直径,AB交CD于O,且AB⊥CD,SO=OB=2,P为SB的中点.(1)求证:SA∥平面PCD;
(2)求圆锥SO的表面积;求圆锥SO的体积.
(3)求异面直线SA与PD所成角的正切值.
考点:异面直线及其所成的角,旋转体(圆柱、圆锥、圆台),直线与平面平行的判定
专题:空间位置关系与距离,空间角
分析:(1)连结PO,由三角形中位线定理得PO∥SA,由此能证明SA∥平面PCD.
(2)由r=2,母线l=SB=2
,由圆锥SO的表面积S表=S侧+S底,圆锥SO的体积V=
S底×SO,由此能求出结果.
(3)由PO∥SA,得∠DPO为异面直线SA与PD所成角,由此能求出异面直线SA与PD所成角的正切值.
(2)由r=2,母线l=SB=2
| 2 |
| 1 |
| 3 |
(3)由PO∥SA,得∠DPO为异面直线SA与PD所成角,由此能求出异面直线SA与PD所成角的正切值.
解答:
(1)证明:连结PO,…(1分)
∵P、O分别为SB、AB的中点,∴PO∥SA,…(2分)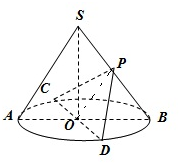
PO?平面PCD,SA不包含于平面PCD,
∴SA∥平面PCD.…(4分)(表述缺漏扣1分)
(2)解:r=2,母线l=SB=2
,…(5分),
S侧=πrl=4
π,…(6分)
∴圆锥SO的表面积S表=S侧+S底=4
π+π•22=4(
+1)π,
圆锥SO的体积V=
S底×SO=
×4π×
=
.…(8分)
(3)解:∵PO∥SA,∴∠DPO为异面直线SA与PD所成角.…(9分)
∵CD⊥AB,CD⊥SO,AB∩SO=O,∴CD⊥平面SOB,…(10分)
∴OD⊥PO.在Rt△DOP中,OD=2,OP=
SB=
,…(11分)
∴tan∠DPO=
=
=
,
∴异面直线SA与PD所成角的正切值为
.…(12分)
∵P、O分别为SB、AB的中点,∴PO∥SA,…(2分)

PO?平面PCD,SA不包含于平面PCD,
∴SA∥平面PCD.…(4分)(表述缺漏扣1分)
(2)解:r=2,母线l=SB=2
| 2 |
S侧=πrl=4
| 2 |
∴圆锥SO的表面积S表=S侧+S底=4
| 2 |
| 2 |
圆锥SO的体积V=
| 1 |
| 3 |
| 1 |
| 3 |
(2
|
| 8π |
| 3 |
(3)解:∵PO∥SA,∴∠DPO为异面直线SA与PD所成角.…(9分)
∵CD⊥AB,CD⊥SO,AB∩SO=O,∴CD⊥平面SOB,…(10分)
∴OD⊥PO.在Rt△DOP中,OD=2,OP=
| 1 |
| 2 |
| 2 |
∴tan∠DPO=
| OD |
| OP |
| 2 | ||
|
| 2 |
∴异面直线SA与PD所成角的正切值为
| 2 |
点评:本题考查直线与平面平行的证明,考查圆锥的表面积和体积的求法,考查异面直线所成角的正切值的求法,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
 如图,已知向量
如图,已知向量| p |
| q |
| π |
| 4 |
| p |
| 2 |
| q |
| AB |
| p |
| q |
| AC |
| p |
| q |
| AD |
A、
| ||||
B、
| ||||
| C、7 | ||||
| D、18 |
 随机抽取某中学高一级学生的一次数学测试成绩得到一样本,其分组区间和频数是:[50,60),2;[60,70);7;[70,80),10;[80,90),x;[90,100],2.其频率分布直方图受到破坏,可见部分如图所示,据此解答如下问题:
随机抽取某中学高一级学生的一次数学测试成绩得到一样本,其分组区间和频数是:[50,60),2;[60,70);7;[70,80),10;[80,90),x;[90,100],2.其频率分布直方图受到破坏,可见部分如图所示,据此解答如下问题: