题目内容
已知数列{an}是公差不为0的等差数列,前n项和为Sn,S5=20,a1,a3,a7成等比数列,数列{
}的前n项和为Tn
(1)求数列{an}的通项公式;
(2)若Tn≤λan+1对一切n∈N*恒成立,求实数λ的最小值;
(3)设cn=(1-
)•
,求证:c1+c2+c3+…+cn<2.
| 1 |
| anan+1 |
(1)求数列{an}的通项公式;
(2)若Tn≤λan+1对一切n∈N*恒成立,求实数λ的最小值;
(3)设cn=(1-
| Tn |
| Tn+1 |
| 1 | ||
|
考点:数列与不等式的综合
专题:等差数列与等比数列
分析:(1)由已知条件利用等差数列的通项公式和等比数列的性质,列出方程组求出首项和公差,由此求出an;
(2)由利用裂项相消法求出数列{
}的前n项和为Tn,不等式条件Tn≤λan+1转化后,利用基本不等式求实数λ的最小值;
(3)有条件和Tn化简cn,根据式子的特点和结论进行放缩,再裂项相消法求出c1+c2+c3+…+cn,再证明结论.
(2)由利用裂项相消法求出数列{
| 1 |
| anan+1 |
(3)有条件和Tn化简cn,根据式子的特点和结论进行放缩,再裂项相消法求出c1+c2+c3+…+cn,再证明结论.
解答:
解:(1)设等差数列{an}的公差为d,
则
,解得
,
∴an=2+n-1=n+1.
(2)由(1)得,
=
=
-
,
则Tn=(
-
)+(
-
)+…+(
-
)
=
-
=
,
∴Tn≤λan+1对一切n∈N*恒成立,
即
≤λ(n+2)对一切n∈N*恒成立,
化简得,λ≥
=
∵n+
≥2
=4,当且仅当n=
时取等号,此时n=2,
∴
≤
,
则实数λ的最小值为
;
(3)由(2)得,Tn=
,则Tn+1=
,
∴cn=(1-
)•
=(1-
)•
=
•
,
∵
=2×(1+
)≤4,
∴cn=
•
≤
=4×(
-
),
∴c1+c2+c3+…+cn≤4[(
-
)+(
-
)+…+((
-
))]
=4(
-
)=2-
<2,
即c1+c2+c3+…+cn<2成立.
则
|
|
∴an=2+n-1=n+1.
(2)由(1)得,
| 1 |
| anan+1 |
| 1 |
| (n+1)(n+2) |
| 1 |
| n+1 |
| 1 |
| n+2 |
则Tn=(
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| n+1 |
| 1 |
| n+2 |
=
| 1 |
| 2 |
| 1 |
| n+2 |
| n |
| 2(n+2) |
∴Tn≤λan+1对一切n∈N*恒成立,
即
| n |
| 2(n+2) |
化简得,λ≥
| n |
| 2(n+2)2 |
| 1 | ||
2(n+
|
∵n+
| 4 |
| n |
n×
|
| 4 |
| n |
∴
| 1 | ||
2(n+
|
| 1 |
| 16 |
则实数λ的最小值为
| 1 |
| 16 |
(3)由(2)得,Tn=
| n |
| 2(n+2) |
| n+1 |
| 2(n+3) |
∴cn=(1-
| Tn |
| Tn+1 |
| 1 | ||
|
| ||
|
|
=
| 2 |
| (n+1)(n+2) |
|
∵
| 2(n+3) |
| n+1 |
| 2 |
| n+1 |
∴cn=
| 2 |
| (n+1)(n+2) |
|
| 4 |
| (n+1)(n+2) |
| 1 |
| n+1 |
| 1 |
| n+2 |
∴c1+c2+c3+…+cn≤4[(
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| n+1 |
| 1 |
| n+2 |
=4(
| 1 |
| 2 |
| 1 |
| n+2 |
| 4 |
| n+2 |
即c1+c2+c3+…+cn<2成立.
点评:本题考查了等差数列的通项公式、前n项和公式,等比数列的性质,利用裂项相消法求数列的前n项和,考查了分利用基本不等式求最值问题,以及放缩法证明不等式成立问题,等价转化思想与综合运算、推理证明能力,属于难题.

练习册系列答案
相关题目
 如图,圆锥SO中,AB、CD为底面圆的两条直径,AB交CD于O,且AB⊥CD,SO=OB=2,P为SB的中点.
如图,圆锥SO中,AB、CD为底面圆的两条直径,AB交CD于O,且AB⊥CD,SO=OB=2,P为SB的中点.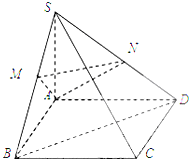 如图,在四棱锥S-ABCD中,SA⊥平面ABCD,底ABCD为正方形M、N分别
如图,在四棱锥S-ABCD中,SA⊥平面ABCD,底ABCD为正方形M、N分别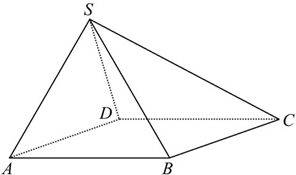 (能力挑战题)如图,已知四棱锥S-ABCD的底面ABCD是菱形,∠BAD=60°,且SA=SB=SD=AB=2.
(能力挑战题)如图,已知四棱锥S-ABCD的底面ABCD是菱形,∠BAD=60°,且SA=SB=SD=AB=2.