题目内容
已知x,y满足
,若z=x+3y的最大值为12,试求k的值.
|
考点:简单线性规划
专题:不等式的解法及应用
分析:对k的取值进行讨论,分k≥0和k<0两种情况进行求解.
解答:
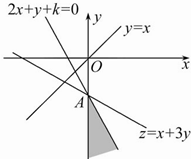 解:由于k的不同取值将影响不等式所表示的平面区域,故应对k的取值进行讨论.
解:由于k的不同取值将影响不等式所表示的平面区域,故应对k的取值进行讨论.
①若k≥0,在平面直角坐标系中画出不等式组所表示的平面区域(如图),由于z=x+3y,所以y=-
x+
z,因此当直线y=-
x+
z经过区域中的点A(0,-k)时,
z取到最大值,等于-3k,令-3k=12,得k=-4,这与k≥0相矛盾,舍去.
②若k<0,在平面直角坐标系中画出不等式组所表示的平面区域(如图),
这时,当直线y=-
x+
z经过区域中的点A(-
,-
)时,z取到最大值,等于-
,
令-
=12,得k=-9.
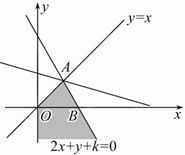
综上,所求k的值为-9.
 解:由于k的不同取值将影响不等式所表示的平面区域,故应对k的取值进行讨论.
解:由于k的不同取值将影响不等式所表示的平面区域,故应对k的取值进行讨论.①若k≥0,在平面直角坐标系中画出不等式组所表示的平面区域(如图),由于z=x+3y,所以y=-
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
z取到最大值,等于-3k,令-3k=12,得k=-4,这与k≥0相矛盾,舍去.
②若k<0,在平面直角坐标系中画出不等式组所表示的平面区域(如图),
这时,当直线y=-
| 1 |
| 3 |
| 1 |
| 3 |
| k |
| 3 |
| k |
| 3 |
| 4k |
| 3 |
令-
| 4k |
| 3 |

综上,所求k的值为-9.
点评:本题主要考查线性规划的应用,利用数形结合是解决线性规划题目的常用方法.考查分类讨论的思想方法.

练习册系列答案
相关题目
双曲线
-
=1的焦距( )
| x2 |
| 64 |
| y2 |
| 36 |
| A、10 | B、16 | C、20 | D、100 |
设
、
、
是空间向量,则“
=x
+y
,(x,y∈R)”是“
、
、
共面”的( )
| p |
| a |
| b |
| p |
| a |
| b |
| p |
| a |
| b |
| A、充分非必要条件 |
| B、必要非充分条件 |
| C、充要条件 |
| D、既非充分也非必要条件 |
设函数y=f(x)在R上有定义,对于任一给定的正数P,定义函数fp(x)=
,则称函数fp(x)为 f(x)的“P界函数”.若给定函数f(x)=x2-2x-1,p=2,则下列结论不成立的是( )
|
| A、fp[f(0)]=f[fp(0)] |
| B、fp[f(1)]=f[fp(1)] |
| C、f[f(2)]=fp[fp(2)]? |
| D、f[f(3)]=fp[fp(3)]? |
 如图,四棱锥S-ABCD的底面是正方形,SD⊥平面ABCD,SD=AD=2,点E是SD的中点.
如图,四棱锥S-ABCD的底面是正方形,SD⊥平面ABCD,SD=AD=2,点E是SD的中点. 如图,圆锥SO中,AB、CD为底面圆的两条直径,AB交CD于O,且AB⊥CD,SO=OB=2,P为SB的中点.
如图,圆锥SO中,AB、CD为底面圆的两条直径,AB交CD于O,且AB⊥CD,SO=OB=2,P为SB的中点.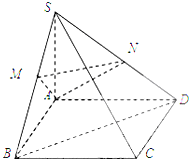 如图,在四棱锥S-ABCD中,SA⊥平面ABCD,底ABCD为正方形M、N分别
如图,在四棱锥S-ABCD中,SA⊥平面ABCD,底ABCD为正方形M、N分别