题目内容
已知矩阵M=
,若向量
在矩阵M的交换下得到向量
(Ⅰ)求矩阵M;
(Ⅱ)矩阵N=
,求直线x+y+1=0在矩阵NM的对应变换作用下得到的曲线方程.
|
|
|
(Ⅰ)求矩阵M;
(Ⅱ)矩阵N=
|
考点:几种特殊的矩阵变换
专题:选作题,矩阵和变换
分析:(Ⅰ)利用矩阵变换公式,即可求矩阵N;
(Ⅱ)求出MN,可得坐标之间的关系,代人直线x+y+1=0整理,即可求曲线的方程.
(Ⅱ)求出MN,可得坐标之间的关系,代人直线x+y+1=0整理,即可求曲线的方程.
解答:
解:(Ⅰ)由
=
…(1分)
得
,解得a=0,b=4…(2分)
∴M=
…(3分)
(Ⅱ)NM=
=
…(4分)
设P(x,y)为x+y+1=0上任一点,在NM变换作用下的对应点为P'(x',y'),
则
=
…(5分)
得
,代入x+y+1=0得y'-5x'+1=0…(6分)
即所求的曲线方程为5x-y-1=0…(7分)
|
|
|
得
|
∴M=
|
(Ⅱ)NM=
|
|
|
设P(x,y)为x+y+1=0上任一点,在NM变换作用下的对应点为P'(x',y'),
则
|
|
|
得
|
即所求的曲线方程为5x-y-1=0…(7分)
点评:本题给出矩阵变换,求直线x+y+1=0在矩阵NM的对应变换作用下得到的曲线方程,着重考查了矩阵与变换的运算、曲线方程的求法等知识,属于中档题.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
边长为4的正方形的直观图的周长为( )
| A、8 | B、12 | C、10 | D、6 |
 如图,圆锥SO中,AB、CD为底面圆的两条直径,AB交CD于O,且AB⊥CD,SO=OB=2,P为SB的中点.
如图,圆锥SO中,AB、CD为底面圆的两条直径,AB交CD于O,且AB⊥CD,SO=OB=2,P为SB的中点.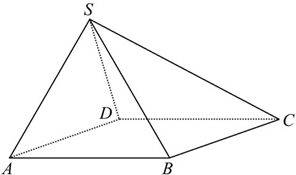 (能力挑战题)如图,已知四棱锥S-ABCD的底面ABCD是菱形,∠BAD=60°,且SA=SB=SD=AB=2.
(能力挑战题)如图,已知四棱锥S-ABCD的底面ABCD是菱形,∠BAD=60°,且SA=SB=SD=AB=2.