题目内容
正方体ABCD-A′B′C′D′棱长为2,E,F,G分别为C′C,D′A′,AB的中点,求点A到平面EFG的距离.
考点:点、线、面间的距离计算
专题:空间位置关系与距离
分析:画出几何体,转化所求距离为A到平面HSG的距离求解即可.
解答:
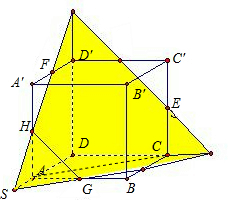 解:由题意E,F,G分别为C′C,D′A′,AB的中点,画出图形如图,则E,F,G是确定的平面如图中的黄色图形,与棱的交点都是所在棱的中点,
解:由题意E,F,G分别为C′C,D′A′,AB的中点,画出图形如图,则E,F,G是确定的平面如图中的黄色图形,与棱的交点都是所在棱的中点,
正方体ABCD-A′B′C′D′棱长为2,易知AC=AH=AS=1,
点A到平面EFG的距离就是A到平面HGS的距离.
HG=HS=SG=
,
设点A到平面EFG的距离为h,则
×
×1×1×1=
×
×(
)2h,
解得h=
.
点A到平面EFG的距离为
.
 解:由题意E,F,G分别为C′C,D′A′,AB的中点,画出图形如图,则E,F,G是确定的平面如图中的黄色图形,与棱的交点都是所在棱的中点,
解:由题意E,F,G分别为C′C,D′A′,AB的中点,画出图形如图,则E,F,G是确定的平面如图中的黄色图形,与棱的交点都是所在棱的中点,正方体ABCD-A′B′C′D′棱长为2,易知AC=AH=AS=1,
点A到平面EFG的距离就是A到平面HGS的距离.
HG=HS=SG=
| 2 |
设点A到平面EFG的距离为h,则
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| ||
| 4 |
| 2 |
解得h=
| ||
| 3 |
点A到平面EFG的距离为
| ||
| 3 |
点评:本题考查点到平面的距离的求法,等体积法的应用,考查空间想象能力以及计算能力.

练习册系列答案
相关题目
方程x+y+z=10的正整数解的个数( )
A、
| ||
B、
| ||
C、
| ||
D、
|
 如图所示,在地面上共线的三点A,B,C处测得一建筑物的仰角分别为30°,45°,60°,且AB=BC=60m,则建筑物的高度为
如图所示,在地面上共线的三点A,B,C处测得一建筑物的仰角分别为30°,45°,60°,且AB=BC=60m,则建筑物的高度为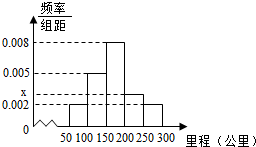 某校研究性学习小组从汽车市场上随机抽取20辆纯电动汽车调查其续驶里程(单次充电后能行驶的最大里程),被调查汽车的续驶里程全部介于50公里和300公里之间,将统计结果分成5组:[50,100),[100,150),[150,200),[200,250),[250,300),绘制成如图所示的频率分布直方图.
某校研究性学习小组从汽车市场上随机抽取20辆纯电动汽车调查其续驶里程(单次充电后能行驶的最大里程),被调查汽车的续驶里程全部介于50公里和300公里之间,将统计结果分成5组:[50,100),[100,150),[150,200),[200,250),[250,300),绘制成如图所示的频率分布直方图.