题目内容
已知向量
=(1,1),向量
与向量
的夹角
,且
•
=-1.
(1)求向量
;
(2)若向量
与向量
=(1,0)的夹角为
,向量
=(cosA,2co2s
),其中ABC为△ABC的内角,且∠C-∠B=∠B-∠A.求|
+
|的取值范围.
| m |
| n |
| m |
| 3π |
| 4 |
| m |
| n |
(1)求向量
| n |
(2)若向量
| n |
| q |
| π |
| 2 |
| p |
| C |
| 2 |
| n |
| p |
考点:平面向量数量积的运算,三角函数中的恒等变换应用
专题:平面向量及应用
分析:(1)利用向量的数量积运算、夹角公式即可得出;
(2)向量
与向量
=(1,0)的夹角为
,可得
=(0,-1).利用∠C-∠B=∠B-∠A,可得∠B=
.向量
=(cosA,2co2s
)=(cosA,1+cosC),可得
+
=(cosA,cosC).于是|
+
|=
=
,利用C∈(0,
),可得cos(
-2C)∈[-
,1].即可得出.
(2)向量
| n |
| q |
| π |
| 2 |
| n |
| π |
| 3 |
| p |
| C |
| 2 |
| n |
| p |
| n |
| p |
| cos2A+cos2C |
1-
|
| 2π |
| 3 |
| 2π |
| 3 |
| 1 |
| 2 |
解答:
解:(1)设
=(x,y),∵向量
=(1,1),向量
与向量
的夹角
,且
•
=-1.
∴cos
=
=
,x+y=-1.
∴|
|=1=
,x+y=-1,
解得
或
.
∴
=(0,-1)或(-1,0).
(2)∵向量
与向量
=(1,0)的夹角为
,∴
=(0,-1).
∵∠C-∠B=∠B-∠A,A+B+C=π,
∴∠B=
.
向量
=(cosA,2co2s
)=(cosA,1+cosC),
∴
+
=(cosA,cosC).
∴|
+
|=
=
=
,
∵C∈(0,
),∴(
-2C)∈(-
,
),
∴cos(
-2C)∈[-
,1].
∴|
+
|∈[
,
].
∴|
+
|的取值范围是[
,
].
| n |
| m |
| n |
| m |
| 3π |
| 4 |
| m |
| n |
∴cos
| 3π |
| 4 |
| ||||
|
|
| -1 | ||||
|
∴|
| n |
| x2+y2 |
解得
|
|
∴
| n |
(2)∵向量
| n |
| q |
| π |
| 2 |
| n |
∵∠C-∠B=∠B-∠A,A+B+C=π,
∴∠B=
| π |
| 3 |
向量
| p |
| C |
| 2 |
∴
| n |
| p |
∴|
| n |
| p |
| cos2A+cos2C |
|
1-
|
∵C∈(0,
| 2π |
| 3 |
| 2π |
| 3 |
| 2π |
| 3 |
| 2π |
| 3 |
∴cos(
| 2π |
| 3 |
| 1 |
| 2 |
∴|
| n |
| p |
| ||
| 2 |
| ||
| 2 |
∴|
| n |
| p |
| ||
| 2 |
| ||
| 2 |
点评:本题考查了向量的数量积运算性质、夹角公式、倍角公式、和差化积、三角函数的单调性,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
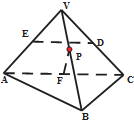 如图所示,正三棱锥V-ABC中,D,E,F分别是VC,VA,AC的中点,P为VB上任意一点,则直线DE与PF所成的角的大小是( )
如图所示,正三棱锥V-ABC中,D,E,F分别是VC,VA,AC的中点,P为VB上任意一点,则直线DE与PF所成的角的大小是( )| A、30° | B、60° |
| C、90° | D、随P点的变化而变化 |
若存在x∈[-2,3],使不等式4x-x2≥a成立,则实数a的取值范围是( )
| A、[-8,+∞) |
| B、[3,+∞) |
| C、(-∞,-12] |
| D、(-∞,4] |
在正三棱锥S-ABC中,M、N分别为SC、BC的中点,且MN⊥AM,若侧棱SA=4,则正三棱锥S-ABC的外接球的表面积是( )
| A、36π | B、72π |
| C、144π | D、48π |