题目内容
已知三棱锥A-BCD的每条棱长都等于1,M为BC中点,N为AD中点.
(1)求AM与BD成的角的余弦;
(2)求AM与CN成的角的余弦.
(1)求AM与BD成的角的余弦;
(2)求AM与CN成的角的余弦.
考点:异面直线及其所成的角,棱锥的结构特征
专题:空间角
分析:(1)取DC中点E,连结ME,AE,则ME∥BD,∠AME是AM与BD成的角(或所成角的补角),由此能求出AM与BD成的角的余弦值.
(2)连结DM,取DM中点F,连结CF、NF,则∠CNF是AM与CN成的角(或所成角的补角),由此能求出AM与CN成的角的余弦值.
(2)连结DM,取DM中点F,连结CF、NF,则∠CNF是AM与CN成的角(或所成角的补角),由此能求出AM与CN成的角的余弦值.
解答:
解:(1)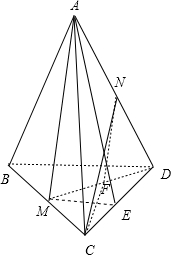 取DC中点E,连结ME,AE,
取DC中点E,连结ME,AE,
∵M是BC中点,∴ME∥BD,
∴∠AME是AM与BD成的角(或所成角的补角),
∵AM=AE=
=
,ME=
,
∴cos∠AME=
=
=
,
∴AM与BD成的角的余弦值为
.
(2)连结DM,取DM中点F,连结CF、NF,
∵N是AD中点,∴NF∥AM,
∴∠CNF是AM与CN成的角(或所成角的补角),
∵DM=CN=
=
,∴NF=
AM=
,
CF=
=
,
∴cos∠CNF=
=
=
,
∴AM与CN成的角的余弦值为
.
 取DC中点E,连结ME,AE,
取DC中点E,连结ME,AE,∵M是BC中点,∴ME∥BD,
∴∠AME是AM与BD成的角(或所成角的补角),
∵AM=AE=
1-
|
| ||
| 2 |
| 1 |
| 2 |
∴cos∠AME=
| AM2+ME2-AE2 |
| 2AM•ME |
| ||||||
2×
|
| ||
| 6 |
∴AM与BD成的角的余弦值为
| ||
| 6 |
(2)连结DM,取DM中点F,连结CF、NF,
∵N是AD中点,∴NF∥AM,
∴∠CNF是AM与CN成的角(或所成角的补角),
∵DM=CN=
1-
|
| ||
| 2 |
| 1 |
| 2 |
| ||
| 4 |
CF=
(
|
| ||
| 4 |
∴cos∠CNF=
| CN2+NF2-CF2 |
| 2×CN×NF |
| ||||||||
2×
|
| 2 |
| 3 |
∴AM与CN成的角的余弦值为
| 2 |
| 3 |
点评:本题考查异面直线所成角的余弦值的求法,是中档题,解题时要认真审题,注意余弦定理的合理运用.

练习册系列答案
相关题目
已知向量
=(2cosφ,2sinφ),φ∈(90°,180°),
=(1,1),则向量
与
的夹角为( )
| a |
| b |
| a |
| b |
| A、φ | B、φ-45° |
| C、135°-φ | D、45°-φ |
