题目内容
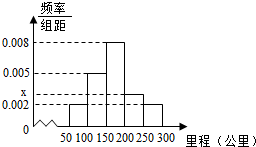 某校研究性学习小组从汽车市场上随机抽取20辆纯电动汽车调查其续驶里程(单次充电后能行驶的最大里程),被调查汽车的续驶里程全部介于50公里和300公里之间,将统计结果分成5组:[50,100),[100,150),[150,200),[200,250),[250,300),绘制成如图所示的频率分布直方图.
某校研究性学习小组从汽车市场上随机抽取20辆纯电动汽车调查其续驶里程(单次充电后能行驶的最大里程),被调查汽车的续驶里程全部介于50公里和300公里之间,将统计结果分成5组:[50,100),[100,150),[150,200),[200,250),[250,300),绘制成如图所示的频率分布直方图.(1)求续驶里程在[200,300]的车辆数;
(2)若从续驶里程在[200,300]的车辆中随机抽取2辆车,求其中恰有一辆车的续驶里程在[200,250)的概率.
考点:频率分布直方图,列举法计算基本事件数及事件发生的概率
专题:算法和程序框图
分析:(1)利用小矩形的面积为1求出x的值;
(2)据直方图求出续驶里程在[200,300]和续驶里程在[250,300)的车辆数,利用排列组合和概率公式求出其中恰有一辆车的续驶里程在[200,250)的概率.
(2)据直方图求出续驶里程在[200,300]和续驶里程在[250,300)的车辆数,利用排列组合和概率公式求出其中恰有一辆车的续驶里程在[200,250)的概率.
解答:
解:(1)有直方图可知0.002×50+0.005×50+0.008×50+x×50+0.002×50=1
解得x=0.003,
续驶里程在[200,300]的车辆数为20×(0.003×50+0.002×50)=5
(2)由题意可知,续驶里程在[200,300]的车辆数为3,
续驶里程在[250,300)的车辆数为2,
从5辆车中随机抽取2辆车,共有
=10中抽法,
其中恰有一辆车的续驶里程在[200,250)的抽法有
=6种,
∴其中恰有一辆车的续驶里程在[200,250)的概率为P(A)=
=
.
解得x=0.003,
续驶里程在[200,300]的车辆数为20×(0.003×50+0.002×50)=5
(2)由题意可知,续驶里程在[200,300]的车辆数为3,
续驶里程在[250,300)的车辆数为2,
从5辆车中随机抽取2辆车,共有
| C | 2 5 |
其中恰有一辆车的续驶里程在[200,250)的抽法有
| C | 1 3 |
| •C | 1 2 |
∴其中恰有一辆车的续驶里程在[200,250)的概率为P(A)=
| 6 |
| 10 |
| 3 |
| 5 |
点评:本题考查直方图、古典概型概率公式;直方图中频率=纵坐标×组距,属于一道基础题.

练习册系列答案
相关题目
在正三棱锥S-ABC中,M、N分别为SC、BC的中点,且MN⊥AM,若侧棱SA=4,则正三棱锥S-ABC的外接球的表面积是( )
| A、36π | B、72π |
| C、144π | D、48π |

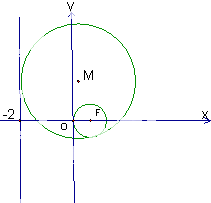 已知:动圆M与圆F:(x-1)2+y2=1内切,且与直线l:x=-2相切,动圆圆心 M的轨迹为曲线Γ
已知:动圆M与圆F:(x-1)2+y2=1内切,且与直线l:x=-2相切,动圆圆心 M的轨迹为曲线Γ