题目内容
函数y=
的图象是由y=
的图象怎样平移得到？
| 1 |
| x |
| -3x-2 |
| x+1 |
考点：函数的图象与图象变化
专题：函数的性质及应用
分析：根据分式函数的性质即可得到两个函数之间的关系．
解答：
解：y=
=
=-3+
，
则将y=
沿着x轴向左平移1个单位得到y=
的图象，
然后将y=
的图象，沿着y轴向下平移3个单位，即可得到y=
的图象．
| -3x-2 |
| x+1 |
| -3(x+1)+1 |
| x+1 |
| 1 |
| x+1 |
则将y=
| 1 |
| x |
| 1 |
| x+1 |
然后将y=
| 1 |
| x+1 |
| -3x-2 |
| x+1 |
点评：本题主要考查函数图象的关系，利用分子常数化是解决本题的关键．
练习册系列答案
相关题目
下列有关命题的说法正确的是（ ）
| A、命题“若x2＞1，则x＞1”的否命题为“若x2＞1，则x≤1” |
| B、“x=-1”是“x2-2x+3=0”的必要不充分条件 |
| C、命题“?x∈R，使得x2+x+1＜0”的否定是“?x∈R，均有x2+x+1＜0” |
| D、命题“若x=y，则cosx=cosy”的逆否命题为真命题 |
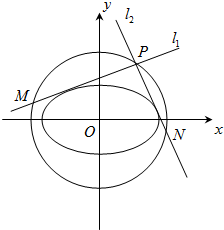给定椭圆C：
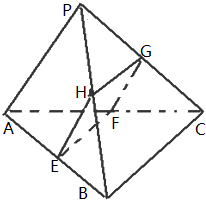如图，已知点P是三角形ABC所在平面外一点，且PA=BC=1，截面EFGH分别平行于PA，BC（点E，F，G，H分在棱AB，AC，PC，PB上）