题目内容
若
<θ<π且cosθ=-
,则sin(θ+
)=( )
| π |
| 2 |
| 3 |
| 5 |
| π |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:两角和与差的正弦函数
专题:计算题,三角函数的求值
分析:运用同角的平方关系和两角和的正弦公式,即可得到所求值.
解答:
解:
<θ<π且cosθ=-
,
则sinθ=
,
sin(θ+
)=
sinθ+
cosθ
=
×
+
×(-
)=
.
故选:B.
| π |
| 2 |
| 3 |
| 5 |
则sinθ=
| 4 |
| 5 |
sin(θ+
| π |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
=
| 1 |
| 2 |
| 4 |
| 5 |
| ||
| 2 |
| 3 |
| 5 |
4-3
| ||
| 10 |
故选:B.
点评:本题考查三角函数的求值,考查两角和的正弦公式和诱导公式的运用,考查运算能力,属于基础题.

练习册系列答案
相关题目
某种商品若每个售价60元,则可卖出50个;已知单价每提高10元,则少卖5个,要得到最大的售货金额,售价应定为( )
| A、80元 | B、85元 |
| C、90元 | D、100元 |
在△ABC中,
=(cos23°,sin23°),
=(2sin22°,2cos22°),则△ABC的面积为( )
| AB |
| AC |
A、2
| ||||
B、
| ||||
C、
| ||||
D、
|
已知函数f(x)=
,若k>0时,方程f(x)=k有且仅有两个不同的实数解x1、x2(x1<x2),则( )
| |sinx| |
| x |
| A、sinx1=-x1•cosx2 |
| B、sinx1=x1•cosx2 |
| C、cosx2=-x2•sinx1 |
| D、cosx2=x2•sinx1 |
“a<2”是“a2-2a<0”的( )
| A、充分非必要条件 |
| B、必要非充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
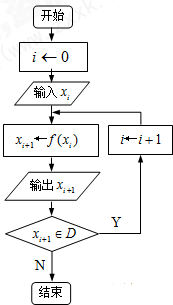 对任意函数f(x),x∈D,可按如图构造一个数列发生器,由数列发生器产生的数列记为{xn}.
对任意函数f(x),x∈D,可按如图构造一个数列发生器,由数列发生器产生的数列记为{xn}.