题目内容
求证:(
)n+(
)n+…+(
)n<
.
| 1 |
| 2n |
| 3 |
| 2n |
| 2n-1 |
| 2n |
| ||
| e-1 |
考点:不等式的证明
专题:证明题,导数的综合应用,等差数列与等比数列,不等式的解法及应用
分析:设函数f(x)=ex-x-1,求出导数,讨论当x<0时,f′(x)<0,f(x)递减.即有x<0时,f(x)>f(0)=0,即有1+x<ex,则
=1-
<e-
=(
)
,即有(
)n<
,同理推出其他项,再运用累加法,对右边运用等比数列求和公式,即可得证.
| 2n-1 |
| 2n |
| 1 |
| 2n |
| 1 |
| 2n |
| 1 | ||
|
| 1 |
| n |
| 2n-1 |
| 2n |
| 1 | ||
|
解答:
证明:设函数f(x)=ex-x-1,导数f′(x)=ex-1,
当x>0时,f′(x)>0,f(x)递增,当x<0时,f′(x)<0,f(x)递减.
即有x<0时,f(x)>f(0)=0,即有1+x<ex,
则
=1-
<e-
=(
)
,即有(
)n<
,
则有(
)n<(
)3,(
)n<(
)5,…,(
)n<(
)2n-1,
即有(
)n+(
)n+…+(
)n<(
)2n-1+(
)2n-3+…+(
)5+(
)3+
=
<
=
.
即不等式成立.
当x>0时,f′(x)>0,f(x)递增,当x<0时,f′(x)<0,f(x)递减.
即有x<0时,f(x)>f(0)=0,即有1+x<ex,
则
| 2n-1 |
| 2n |
| 1 |
| 2n |
| 1 |
| 2n |
| 1 | ||
|
| 1 |
| n |
| 2n-1 |
| 2n |
| 1 | ||
|
则有(
| 2n-3 |
| 2n |
| 1 | ||
|
| 2n-5 |
| 2n |
| 1 | ||
|
| 1 |
| 2n |
| 1 | ||
|
即有(
| 1 |
| 2n |
| 3 |
| 2n |
| 2n-1 |
| 2n |
| 1 | ||
|
| 1 | ||
|
| 1 | ||
|
| 1 | ||
|
| 1 | ||
|
=
| ||||||
1-
|
| ||||
1-
|
| ||
| e-1 |
即不等式成立.
点评:本题考查导数的运用:求单调性,考查不等式的证明方法:运用已知不等式,借助等比数列的求和公式,考查运算能力,属于难题.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
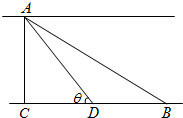 如图,一条河的两岸是平行线,两岸边各有一个小镇A与B,它们的直线距离为2km,河宽AC=1km,根据规划,需要在两岸间铺设一条电缆线,从A处铺设水下电缆到D处(D为线段BC上的点),再从D处铺设地下电缆到B处,已知铺设水下电缆的费用是铺设地下电缆费用的2倍,记∠ADC=θ.
如图,一条河的两岸是平行线,两岸边各有一个小镇A与B,它们的直线距离为2km,河宽AC=1km,根据规划,需要在两岸间铺设一条电缆线,从A处铺设水下电缆到D处(D为线段BC上的点),再从D处铺设地下电缆到B处,已知铺设水下电缆的费用是铺设地下电缆费用的2倍,记∠ADC=θ.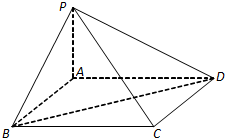 如图,在四棱锥P-ABCD中,底面ABCD是菱形,且PB=PD.
如图,在四棱锥P-ABCD中,底面ABCD是菱形,且PB=PD.