题目内容
甲、乙、丙三人独立破译一种密码,他们破译成功的概率分别为
,
,
求:
(1)三人同时破译,恰有一人破译成功的概率;
(2)三人同时破译,能破译成功的概率;
(3)要使破译成功的概率不小于95%,至少需要丙这样的人多少个?
| 1 |
| 2 |
| 3 |
| 5 |
| 3 |
| 4 |
(1)三人同时破译,恰有一人破译成功的概率;
(2)三人同时破译,能破译成功的概率;
(3)要使破译成功的概率不小于95%,至少需要丙这样的人多少个?
考点:相互独立事件的概率乘法公式,互斥事件的概率加法公式
专题:概率与统计
分析:设A,B,C分别表示甲,乙,丙破译成功,则P(A)=
,P(B)=
,P(C)=
.
(1)分三种情况求得恰有一人破译成功的概率,再把这3个概率值相加,即得所求.
(2)三人同时破译,先求出不能破译成功的概率,再用1减去此概率,即得所求.
(3)设需丙这样的人n个,1-(1-
)n≥
,求得n的范围,可得结论.
| 1 |
| 2 |
| 3 |
| 5 |
| 3 |
| 4 |
(1)分三种情况求得恰有一人破译成功的概率,再把这3个概率值相加,即得所求.
(2)三人同时破译,先求出不能破译成功的概率,再用1减去此概率,即得所求.
(3)设需丙这样的人n个,1-(1-
| 3 |
| 4 |
| 95 |
| 100 |
解答:
解:设A,B,C分别表示甲,乙,丙破译成功,则P(A)=
,P(B)=
,P(C)=
.
(1)恰有一人破译成功的概率P=
×(1-
)×(1-
)+(1-
)×
×(1-
)+(1-
)×(1-
)×
=
.
(2)三人同时破译,不能破译成功的概率为(1-
)(1-
)(1-
)=
,
∴三人同时破译,能破译成功的概率为1-
=
.
(3)设需丙这样的人n个,1-(1-
)n≥
,得 n≥3,故至少需丙这样的人3个.
| 1 |
| 2 |
| 3 |
| 5 |
| 3 |
| 4 |
(1)恰有一人破译成功的概率P=
| 1 |
| 2 |
| 3 |
| 5 |
| 3 |
| 4 |
| 1 |
| 2 |
| 3 |
| 5 |
| 3 |
| 4 |
| 1 |
| 2 |
| 3 |
| 5 |
| 3 |
| 4 |
| 11 |
| 40 |
(2)三人同时破译,不能破译成功的概率为(1-
| 1 |
| 2 |
| 3 |
| 5 |
| 3 |
| 4 |
| 1 |
| 20 |
∴三人同时破译,能破译成功的概率为1-
| 1 |
| 20 |
| 19 |
| 20 |
(3)设需丙这样的人n个,1-(1-
| 3 |
| 4 |
| 95 |
| 100 |
点评:本题主要考查相互独立事件的概率乘法公式,所求的事件的概率与它的对立事件的概率之间的关系,属于基础题.

练习册系列答案
相关题目
圆心在直线x=2上的圆C与y轴交于两点A(0,-4),B(0,-2),则圆C的方程为( )
| A、(x-2)2+(y-3)2=5 |
| B、(x-2)2+(y-3)2=25 |
| C、(x-2)2+(y+3)2=5 |
| D、(x-2)2+(y+3)2=25 |
设x,y满足的约束条件是
,则z=x+2y的最小值是( )
|
| A、-1 | B、3 | C、5 | D、6 |
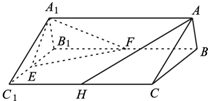 如图,在直三棱柱ABC-A1B1C1中,AB=AC=1,AA1=2,E、F分别是棱B1C1、B1B的中点,H在棱CC1上,且AB⊥AH.
如图,在直三棱柱ABC-A1B1C1中,AB=AC=1,AA1=2,E、F分别是棱B1C1、B1B的中点,H在棱CC1上,且AB⊥AH.