题目内容
已知a>0,b>0,求证下列各式:
(1)
≥
.
(2)a+b≥
+
.
(1)
|
| a+b |
| 2 |
(2)a+b≥
| ab |
|
考点:不等式的证明
专题:证明题,不等式的解法及应用
分析:(1)利用a+b>0且a2+b2≥2ab,即可证明
≥
.
(2)由(1)可知,a+b≤2
,可得
+
≤2
=a+b,即可证明a+b≥
+
.
|
| a+b |
| 2 |
(2)由(1)可知,a+b≤2
|
| ab |
|
|
| ab |
|
解答:
证明:(1)∵a>0,b>0,∴a+b>0且a2+b2≥2ab…(1分)
∴
≥
=
(当且仅当a=b时等号成立) …(5分)
∴
≥
…(6分)
(2)∵a>0,b>0,∴由(1)可知,a+b≤2
…(7分)
∴
+
≤2
=a+b…(9分)
当且仅当
=
即a=b时等号成立 …(11分)
∴a+b≥
+
…(12分)
∴
|
|
| a+b |
| 2 |
∴
|
| a+b |
| 2 |
(2)∵a>0,b>0,∴由(1)可知,a+b≤2
|
∴
| ab |
|
|
当且仅当
| ab |
|
∴a+b≥
| ab |
|
点评:本题考查不等式的证明,考查基本不等式的运用,难度中等.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
曲线y=x3+x-2在点P0处的切线平行于直线y=4x-1,则点P0的坐标是( )
| A、(0,1) |
| B、(-1,-5) |
| C、(1,0)或(-1,-4) |
| D、(0,1)或(4,1) |
设等差数列{an}的前n项和为Sn,若S3=9,S9=36,则a7+a8+a9等于( )
| A、15 | B、12 | C、36 | D、27 |
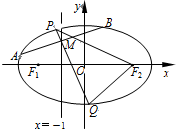 如图,F1、F2是离心率为
如图,F1、F2是离心率为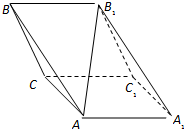 如图,斜三棱柱ABC-A1B1C1,已知侧面BB1C1C与底面ABC垂直且∠BCA=90°,∠B1BC=60°,BC=BB1=2,若二面角A-B1B-C为30°,
如图,斜三棱柱ABC-A1B1C1,已知侧面BB1C1C与底面ABC垂直且∠BCA=90°,∠B1BC=60°,BC=BB1=2,若二面角A-B1B-C为30°,