题目内容
4.函数f(x)=$\frac{{{e^x}+1}}{{{e^x}-1}}$•cosx的图象大致是( )| A. |  | B. |  | C. |  | D. |  |
分析 判断函数的奇偶性,排除选项,利用特殊点的位置判断即可.
解答 解:函数f(x)=$\frac{{{e^x}+1}}{{{e^x}-1}}$•cosx,可知:f(-x)=$\frac{{e}^{-x}+1}{{e}^{-x}-1}$•cosx=-$\frac{{{e^x}+1}}{{{e^x}-1}}$•cosx=-f(x),函数是奇函数.
排除A、B,当x∈(0,$\frac{π}{2}$)时,f(x)>0,排除D,
故选:C.
点评 本题考查函数的图象的判断与应用,函数的奇偶性与特殊点位置是判断函数的图形的常用方法.

练习册系列答案
相关题目
15.已知集合A={x∈N|-2<x<4},$B=\{x|\frac{1}{2}≤{2^x}≤4\}$,则A∩B=( )
| A. | {x|-1≤x≤2} | B. | {-1,0,1,2} | C. | {1,2} | D. | {0,1,2} |
12.我国古代名著《九章算术》中有这样一段话:“今有金锤,长五尺,斩本一尺,重四斤.斩末一尺,重二斤.”意思是:“现有一根金锤,头部的1尺,重4斤;尾部的1尺,重2斤;且从头到尾,每一尺的重量构成等差数列.”则下列说法错误的是( )
| A. | 该金锤中间一尺重3斤 | |
| B. | 中间三尺的重量和是头尾两尺重量和的3倍 | |
| C. | 该金锤的重量为15斤 | |
| D. | 该金锤相邻两尺的重量之差的绝对值为0.5斤 |
19.已知集合A={x|x<a},B={x|x2-3x+2<0},若A∩B=B,则实数a的取值范围是( )
| A. | a≤1 | B. | a<1 | C. | a≥2 | D. | a>2 |
16.在一次实验中,同时抛掷4枚均匀的硬币16次,设4枚硬币正好出现3枚正面向上,1枚反面向上的次数为ξ,则ξ的方差是( )
| A. | 3 | B. | 4 | C. | 1 | D. | $\frac{15}{16}$ |
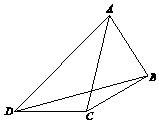 在如图所示的平面图形中,已知CD=$\sqrt{2}$,∠BCA=45°,∠ACD=105°,∠CDB=15°,∠BDA=30°.
在如图所示的平面图形中,已知CD=$\sqrt{2}$,∠BCA=45°,∠ACD=105°,∠CDB=15°,∠BDA=30°.