题目内容
19.已知集合A={x|x<a},B={x|x2-3x+2<0},若A∩B=B,则实数a的取值范围是( )| A. | a≤1 | B. | a<1 | C. | a≥2 | D. | a>2 |
分析 化简集合B,根据A∩B=B,建立条件关系即可求实数a的取值范围.
解答 解:由题意,集合A={x|x<a},B={x|x2-3x+2<0}={x|1<x<2},
∵A∩B=B,
∴B⊆A,
则:a≥2.
∴实数a的取值范围[2,+∞).
故选C.
点评 本题主要考查集合的基本运算,比较基础.

练习册系列答案
相关题目
8.若双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的渐近线将圆x2+y2-2x-4y+4=0平分,则双曲线的离心率为( )
| A. | 3 | B. | $\sqrt{5}$ | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
9.在封闭直三棱柱ABC-A1B1C1内有一个体积为V的球,若AB⊥BC,AB=15,BC=8,AA1=5,则V的最大值是( )
| A. | $\frac{9π}{2}$ | B. | $\frac{125π}{6}$ | C. | $\frac{32π}{3}$ | D. | 36π |
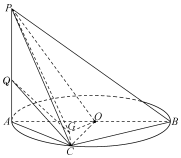 如图,点C在以AB为直径的圆O上,PA垂直与圆O所在平面,G为△AOC的垂心.
如图,点C在以AB为直径的圆O上,PA垂直与圆O所在平面,G为△AOC的垂心. 如图所示,在三棱柱ABC-A1B1C1中,AA1B1B为正方形,BB1C1C为菱形,B1C⊥AC1.
如图所示,在三棱柱ABC-A1B1C1中,AA1B1B为正方形,BB1C1C为菱形,B1C⊥AC1.


