题目内容
已知函数f(x)=-x2+ax定义在区间[0,1]上的函数列,fn(x)(n=1,2,3,…)满足f1(x)=4f(x),fn+1=f1(fn(x))(n=1,2,3,…),且fn(x)在[0,1]上的最大值为1,最小值为0.
(1)设fn(x)在[0,1]上取得最大值时x的值的个数为an,求实数a的值;
(2)数列{an}的前n项的和为Sn,求Sn的解析式.
(1)设fn(x)在[0,1]上取得最大值时x的值的个数为an,求实数a的值;
(2)数列{an}的前n项的和为Sn,求Sn的解析式.
考点:数列与函数的综合
专题:等差数列与等比数列
分析:(1)由题意根据归纳推理得出a1=1,a2=2,a3=4,…an=2n-1,
(2)利用等比数列求和公式解得即可.
(2)利用等比数列求和公式解得即可.
解答:
解:(1)由由题意得f1(x)=4f(x)=-4x2+4ax,
∴f1′(x)=-8x+4a=0时,x=
,
∴f1(0)=0,f1(1)=-4+4a,f1(
)=a2,
∵f1(x)在[0,1]上的最大值为1,最小值为0.
∴最大值为:a2=1,解得a=1或a=-1(舍去).
∴f1(x)=-4x2+4x,当x=
时取得最大值1,则a1=1,
又fn+1=f1(fn(x)),
∴f2=f1(f1(x))=-4(f1(x))2+4f1(x)=1,
∴f1(x)=-4x2+4x,方程有两个解x1,x2,(如图)A,B横坐标,则a2=2,

由f3=f1(f2(x))=f1(f1(f1(x)))=1,
∴f1(f1(x))=
,∴f1(x)=x1,或f1(x)=x2,
∴-4x2+4x=x1或-4x2+4x=x2可解得4个解,如图DEFG横坐标,则a3=4,
同理fn(x)在[0,1]上取得最大值时x的值的个数为an=2n-1.
(2)sn=1+2+4+…+2n-1=
=2n-1.
∴f1′(x)=-8x+4a=0时,x=
| a |
| 2 |
∴f1(0)=0,f1(1)=-4+4a,f1(
| a |
| 2 |
∵f1(x)在[0,1]上的最大值为1,最小值为0.
∴最大值为:a2=1,解得a=1或a=-1(舍去).
∴f1(x)=-4x2+4x,当x=
| 1 |
| 2 |
又fn+1=f1(fn(x)),
∴f2=f1(f1(x))=-4(f1(x))2+4f1(x)=1,
∴f1(x)=-4x2+4x,方程有两个解x1,x2,(如图)A,B横坐标,则a2=2,

由f3=f1(f2(x))=f1(f1(f1(x)))=1,
∴f1(f1(x))=
| 1 |
| 2 |
∴-4x2+4x=x1或-4x2+4x=x2可解得4个解,如图DEFG横坐标,则a3=4,
同理fn(x)在[0,1]上取得最大值时x的值的个数为an=2n-1.
(2)sn=1+2+4+…+2n-1=
| 1-2n |
| 1-2 |
点评:本题主要考查利用递推公式求数列的通项公式及等比数列求和知识,考查学生分析问题、解决问题的能力及运算求解能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知p:m-1<x<m+1,q:(x-2)(x-6)<0,且q是p的必要不充分条件,则m的取值范围是( )
| A、3<m<5 |
| B、3≤m≤5 |
| C、m>5或m<3 |
| D、m≥5或m≤3 |
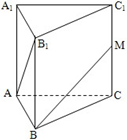 如图,已知三棱柱ABC-A1B1C1的各条棱长都相等,且CC1⊥底面ABC,M是侧棱CC1的中点,则异面直线AB1和BM所成的角的大小是( )
如图,已知三棱柱ABC-A1B1C1的各条棱长都相等,且CC1⊥底面ABC,M是侧棱CC1的中点,则异面直线AB1和BM所成的角的大小是( )