题目内容
 已知F1,F2是椭圆
已知F1,F2是椭圆| x2 |
| 2 |
| y2 |
| 4 |
| PF1 |
| PF2 |
(1)求点P坐标;
(2)求证:直线AB的斜率为定值;
(3)求△PAB面积的最大值.
考点:直线与圆锥曲线的关系,平面向量数量积的运算
专题:计算题,平面向量及应用,直线与圆,圆锥曲线的定义、性质与方程
分析:(1)求出椭圆的两焦点坐标,设P(x,y),(x>0,y>0),由数量积坐标公式和点在椭圆上,列出方程,解出,即可得到P的坐标;
(2)设出直线PA,PB的方程,联立椭圆方程,消去y,得到x的二次方程,运用韦达定理,即可解得A,B的横坐标,再由直线方程,得到纵坐标,再由斜率公式,即可得证;
(3)设出直线AB的方程,联立椭圆方程,消去y,得到x的方程,运用韦达定理,以及弦长公式和点到直线的距离公式,再由面积公式,运用基本不等式,即可得到最大值.
(2)设出直线PA,PB的方程,联立椭圆方程,消去y,得到x的二次方程,运用韦达定理,即可解得A,B的横坐标,再由直线方程,得到纵坐标,再由斜率公式,即可得证;
(3)设出直线AB的方程,联立椭圆方程,消去y,得到x的方程,运用韦达定理,以及弦长公式和点到直线的距离公式,再由面积公式,运用基本不等式,即可得到最大值.
解答:
(1)解:F1,F2是椭圆
+
=1的两焦点,
则c=
=
,即有F1(0,
),F2(0,-
),设P(x,y),(x>0,y>0),
则由
•
=1,得x2+y2=3,又
+
=1,解得,x=1,y=
.
则有点P的坐标为(1,
);
(2)证明:由题意知,两直线PA、PB的斜率必存在,
设直线PB的斜率为k,则直线PB的方程为y-
=k(x-1),
由于过点P作倾斜角互补的两条直线PA、PB,则直线PA:y-
=-k(x-1).
由
,消去y,得(2+k2)x2+2k(
-k)x+(
-k)2-4=0,
设A(xA,yA),B(xB,yB),由韦达定理,得1+xB=
,
即有xB=
,yB=
同理可得xA=
,yA=
,
所以kAB=
=
为定值.
(3)解:由(2)可设直线AB的方程为y=
x+m,
联立方程,得
,消去y,得4x2+2
mx+m2-4=0,
由判别式8m2-16(m2-4)>0,得m∈(-2
,2
),x1+x2=-
m,x1x2=
,
|AB|=
=
易知点P到直线AB的距离为d=
,
所以S△PAB=
|AB|•d=
≤
,
当且仅当m=±2时取等号,满足m∈(-2
,2
),
所以△PAB面积的最大值为
.
| x2 |
| 2 |
| y2 |
| 4 |
则c=
| 4-2 |
| 2 |
| 2 |
| 2 |
则由
| PF1 |
| PF2 |
| x2 |
| 2 |
| y2 |
| 4 |
| 2 |
则有点P的坐标为(1,
| 2 |
(2)证明:由题意知,两直线PA、PB的斜率必存在,
设直线PB的斜率为k,则直线PB的方程为y-
| 2 |
由于过点P作倾斜角互补的两条直线PA、PB,则直线PA:y-
| 2 |
由
|
| 2 |
| 2 |
设A(xA,yA),B(xB,yB),由韦达定理,得1+xB=
-2k(
| ||
| 2+k2 |
即有xB=
k2-2
| ||
| 2+k2 |
2
| ||||
| 2+k2 |
同理可得xA=
k2+2
| ||
| 2+k2 |
2
| ||||
| 2+k2 |
所以kAB=
| yA-yB |
| xA-xB |
| 2 |
(3)解:由(2)可设直线AB的方程为y=
| 2 |
联立方程,得
|
| 2 |
由判别式8m2-16(m2-4)>0,得m∈(-2
| 2 |
| 2 |
| ||
| 2 |
| m2-4 |
| 4 |
|AB|=
| (1+2)((x1+x2)2-4x1x2) |
3(
|
易知点P到直线AB的距离为d=
| |m| | ||
|
所以S△PAB=
| 1 |
| 2 |
|
| 2 |
当且仅当m=±2时取等号,满足m∈(-2
| 2 |
| 2 |
所以△PAB面积的最大值为
| 2 |
点评:本题考查椭圆的方程和性质及运用,考查平面向量的数量积的坐标该函数,考查联立直线方程和椭圆方程,运用韦达定理,和弦长公式解题,考查直线的斜率和方程的运用,同时考查点到直线的距离公式,考查运算化简能力,属于中档题.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
正方体的外接球与其内切球的体积之比为 ( )
A、
| ||
| B、3:1 | ||
C、3
| ||
| D、9:1 |
在△ABC中,角A、B、C所对的边分别为a、b、c,若a•cosA=bcosB,则△ABC的形状为( )
| A、等腰三角形 |
| B、直角三角形 |
| C、等腰三角形或直角三角形 |
| D、等腰直角三角形 |
 已知:如图所示,l1∩l2=A,l2∩l3=B,l1∩l3=C.求证:直线l1,l2,l3在同一平面内.
已知:如图所示,l1∩l2=A,l2∩l3=B,l1∩l3=C.求证:直线l1,l2,l3在同一平面内.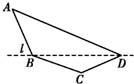 某单位设计一个展览沙盘,现欲在沙盘平面内,铺设一个对角线在L上的四边形电气线路,如图所示.为充分利用现有材料,边BC,CD用一根5米长的材料弯折而成,边BA,AD用一根9米长的材料弯折而成,使A+C=180°,且AB=BC.设AB=x米,cos A=f(x).
某单位设计一个展览沙盘,现欲在沙盘平面内,铺设一个对角线在L上的四边形电气线路,如图所示.为充分利用现有材料,边BC,CD用一根5米长的材料弯折而成,边BA,AD用一根9米长的材料弯折而成,使A+C=180°,且AB=BC.设AB=x米,cos A=f(x).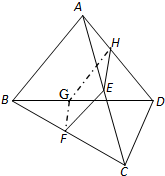 如图,在四面体ABCD中,平行于AB,CD的平面β截四面体所得截面为EFGH.
如图,在四面体ABCD中,平行于AB,CD的平面β截四面体所得截面为EFGH.