题目内容
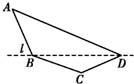 某单位设计一个展览沙盘,现欲在沙盘平面内,铺设一个对角线在L上的四边形电气线路,如图所示.为充分利用现有材料,边BC,CD用一根5米长的材料弯折而成,边BA,AD用一根9米长的材料弯折而成,使A+C=180°,且AB=BC.设AB=x米,cos A=f(x).
某单位设计一个展览沙盘,现欲在沙盘平面内,铺设一个对角线在L上的四边形电气线路,如图所示.为充分利用现有材料,边BC,CD用一根5米长的材料弯折而成,边BA,AD用一根9米长的材料弯折而成,使A+C=180°,且AB=BC.设AB=x米,cos A=f(x).(1)求f(x)的解析式,并指出x的取值范围;
(2)求y=
| sinA |
| AB |
考点:解三角形的实际应用
专题:应用题,解三角形
分析:(1)利用余弦定理,建立方程,解得cos A=
,即可求f(x)的解析式,并指出x的取值范围;
(2)表示出y=
,利用基本不等式求出最大值,并指出相应的x值.
| 2 |
| x |
(2)表示出y=
| sinA |
| AB |
解答:
解:(1)在△ABD中,由余弦定理得BD2=AB2+AD2-2AB•AD•cosA.
同理,在△CBD中,BD2=CB2+CD2-2CB•CD•cosC.
因为∠A和∠C互补,
所以AB2+AD2-2AB•AD•cosA=CB2+CD2-2CB•CD•cosC=CB2+CD2+2CB•CD•cosA.…(4分)
即x2+(9-x)2-2x(9-x)cosA=x2+(5-x)2+2x(5-xcosA.
解得cosA=
,
即f(x)=
,其中x∈(2,5)…(7分)
(2)由(1)知,sinA=
,∴y=
x∈(2,5)…(9分)
∴y=
•
≤
•
=
,…(11分)
当
=1-
⇒x2=8⇒x=2
时,ymax=
…(13分)
同理,在△CBD中,BD2=CB2+CD2-2CB•CD•cosC.
因为∠A和∠C互补,
所以AB2+AD2-2AB•AD•cosA=CB2+CD2-2CB•CD•cosC=CB2+CD2+2CB•CD•cosA.…(4分)
即x2+(9-x)2-2x(9-x)cosA=x2+(5-x)2+2x(5-xcosA.
解得cosA=
| 2 |
| x |
即f(x)=
| 2 |
| x |
(2)由(1)知,sinA=
1-
|
| 1 |
| x |
1-
|
∴y=
| 1 |
| 2 |
| 2 |
| x |
1-
|
| 1 |
| 2 |
| ||||
| 2 |
| 1 |
| 4 |
当
| 4 |
| x2 |
| 4 |
| x2 |
| 2 |
| 1 |
| 4 |
点评:本题考查余弦定理,考查基本不等式的运用,正确运用余弦定理是关键.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目

 已知F1,F2是椭圆
已知F1,F2是椭圆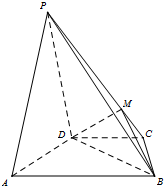 如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,AB∥DC,PD=PA,已知AB=2DC=10,BD=
如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,AB∥DC,PD=PA,已知AB=2DC=10,BD=