题目内容
有下列命题:
①双曲线
-
=1与椭圆
+y2=1有相同的焦点;
②“-
<x<0”是“2x2-5x-3<0”必要不充分条件;
③若
、
共线,则
、
所在的直线平行;
④?x∈R,x2-3x+3≠0.
其中是真命题的有: .
①双曲线
| x2 |
| 25 |
| y2 |
| 9 |
| x2 |
| 35 |
②“-
| 1 |
| 2 |
③若
| a |
| b |
| a |
| b |
④?x∈R,x2-3x+3≠0.
其中是真命题的有:
考点:命题的真假判断与应用
专题:不等式的解法及应用,平面向量及应用,圆锥曲线的定义、性质与方程
分析:本题可以利用椭圆方程、不等式化简、向量的几何意义等知识对4个命题分别进行判断,确定其真假,得到本题结论.
解答:
解:关于命题①
∵双曲线
-
=1中,a2=25,b2=9
∴c2=a2+b2=34,c=
.
∴双曲线
-
=1的焦点坐标为(±
,0).
∵椭圆
+y2=1中,a′2=35,b′2=1,
∴c′2=a′2-b′2=35-1=34,c′=
.
∴椭圆
+y2=1的焦点坐标为(±
,0).
∴双曲线
-
=1与椭圆
+y2=1有相同的焦点.
故命题①正确;
关于命题②
∵2x2-5x-3<0,
?(2x+1)(x-3)<0,
?-
<x<3.
又∵“-
<x<0”⇒“-
<x<3”,反之不成立,
∴“-
<x<0”是“2x2-5x-3<0”充分不必要条件;
故命题②错误;
关于命题③
若
、
共线,
则
∥
.
∴
、
所在的直线平行或者共线,
故命题③错误;
关于命题④
?x∈R,
x2-3x+3=(x-
)2+3-
=(x-
)2+
≥
,
∴x2-3x+3≠0,
故命题④正确.
综上,正确的命题有:①④.
故答案为:①④.
∵双曲线
| x2 |
| 25 |
| y2 |
| 9 |
∴c2=a2+b2=34,c=
| 34 |
∴双曲线
| x2 |
| 25 |
| y2 |
| 9 |
| 34 |
∵椭圆
| x2 |
| 35 |
∴c′2=a′2-b′2=35-1=34,c′=
| 34 |
∴椭圆
| x2 |
| 35 |
| 34 |
∴双曲线
| x2 |
| 25 |
| y2 |
| 9 |
| x2 |
| 35 |
故命题①正确;
关于命题②
∵2x2-5x-3<0,
?(2x+1)(x-3)<0,
?-
| 1 |
| 2 |
又∵“-
| 1 |
| 2 |
| 1 |
| 2 |
∴“-
| 1 |
| 2 |
故命题②错误;
关于命题③
若
| a |
| b |
则
| a |
| b |
∴
| a |
| b |
故命题③错误;
关于命题④
?x∈R,
x2-3x+3=(x-
| 3 |
| 2 |
| 9 |
| 4 |
| 3 |
| 2 |
| 3 |
| 4 |
| 3 |
| 4 |
∴x2-3x+3≠0,
故命题④正确.
综上,正确的命题有:①④.
故答案为:①④.
点评:本题考查了椭圆方程、不等式化简、向量的几何意义等知识,本题难度适中,属于中档题.

练习册系列答案
相关题目
设全集U=R,集合A={x|x<0},B={x|-1<x<3},则A∩B=( )
| A、{x|-1<x<0} |
| B、{x|0<x<3} |
| C、{x|x<0} |
| D、{x|x<3} |
 已知F1,F2是椭圆
已知F1,F2是椭圆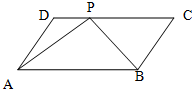 如图,在四边形ABCD中,
如图,在四边形ABCD中,