题目内容
函数y=f(x)定义域为R,其图象是连续不断的,若存在非零实数k使得f(x+k)+kf(x)=0对任意x∈R恒成立,称y=f(x)是一个“k阶伴随函数”,k称函数y=f(x)的“伴随值”.下列结论正确的是
①k=-1是任意常数函数f(x)=c(c为常数)的“伴随值”;
②f(x)=x2是一个“k阶伴随函数”;
③“1阶伴随函数”y=f(x)是周期函数,且1是函数y=f(x)的一个周期;
④f(x)=sin(πx+
)是一个“k阶伴随函数”;
⑤任意“k(k>0)阶伴随函数”y=f(x)一定存在零点.
①k=-1是任意常数函数f(x)=c(c为常数)的“伴随值”;
②f(x)=x2是一个“k阶伴随函数”;
③“1阶伴随函数”y=f(x)是周期函数,且1是函数y=f(x)的一个周期;
④f(x)=sin(πx+
| π |
| 3 |
⑤任意“k(k>0)阶伴随函数”y=f(x)一定存在零点.
考点:抽象函数及其应用
专题:计算题,阅读型,函数的性质及应用
分析:①f(x-1)-f(x)=c-c=0,
②f(x+k)+kf(x)=(x+k)2+kx2=0,则(1+k)x2+2kx+k2=0对任意x∈R恒成立,则
,无解;
③由f(x+1)+f(x)=0可得f(x)=-f(x+1)=f(x+2);
④由sin(π+a)=-sina可推出f(x+1)+f(x)=0,
⑤由f(x+k)+kf(x)=0对任意x∈R恒成立,且k>0可得f(x+k)=f(x)=0,或f(x+k)•f(x)<0.
②f(x+k)+kf(x)=(x+k)2+kx2=0,则(1+k)x2+2kx+k2=0对任意x∈R恒成立,则
|
③由f(x+1)+f(x)=0可得f(x)=-f(x+1)=f(x+2);
④由sin(π+a)=-sina可推出f(x+1)+f(x)=0,
⑤由f(x+k)+kf(x)=0对任意x∈R恒成立,且k>0可得f(x+k)=f(x)=0,或f(x+k)•f(x)<0.
解答:
解:若f(x)=c(c为常数),k=-1,则f(x-1)-f(x)=c-c=0,故①正确;
若f(x+k)+kf(x)=(x+k)2+kx2=0,
则(1+k)x2+2kx+k2=0对任意x∈R恒成立,则
,无解;故②错误;
由y=f(x)是“1阶伴随函数”,则f(x+1)+f(x)=0,
则f(x)=-f(x+1)=f(x+2),则2是函数y=f(x)的一个周期,故③错误;
∵f(x+1)=sin(π(x+1)+
)=-sin(πx+
)=-f(x),
∴f(x+1)+f(x)=0,
∴f(x)=sin(πx+
)是一个“1阶伴随函数”;故④正确;
∵f(x+k)+kf(x)=0对任意x∈R恒成立,且k>0,
∴f(x+k)=f(x)=0,或f(x+k)•f(x)<0,
又∵函数y=f(x)定义域为R,其图象是连续不断的,
∴y=f(x)一定存在零点,故⑤正确;
故答案为:①④⑤.
若f(x+k)+kf(x)=(x+k)2+kx2=0,
则(1+k)x2+2kx+k2=0对任意x∈R恒成立,则
|
由y=f(x)是“1阶伴随函数”,则f(x+1)+f(x)=0,
则f(x)=-f(x+1)=f(x+2),则2是函数y=f(x)的一个周期,故③错误;
∵f(x+1)=sin(π(x+1)+
| π |
| 3 |
| π |
| 3 |
∴f(x+1)+f(x)=0,
∴f(x)=sin(πx+
| π |
| 3 |
∵f(x+k)+kf(x)=0对任意x∈R恒成立,且k>0,
∴f(x+k)=f(x)=0,或f(x+k)•f(x)<0,
又∵函数y=f(x)定义域为R,其图象是连续不断的,
∴y=f(x)一定存在零点,故⑤正确;
故答案为:①④⑤.
点评:本题考查了学生对新知识的接受能力及转化能力,属于中档题.

练习册系列答案
相关题目
在△ABC中,AB=4,BC=3,∠ABC=90°,若使△ABC绕直线BC旋转一周,则所形成的几何体的体积是( )
| A、36π | B、28π |
| C、20π | D、16π |
 已知F1,F2是椭圆
已知F1,F2是椭圆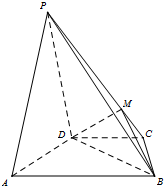 如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,AB∥DC,PD=PA,已知AB=2DC=10,BD=
如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,AB∥DC,PD=PA,已知AB=2DC=10,BD=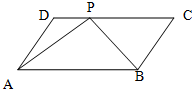 如图,在四边形ABCD中,
如图,在四边形ABCD中,