题目内容
9.已知函数f(x)=ax+lnx,其中a为常数,设e为自然对数的底数.(1)当a=-1时,求f(x)的最大值;
(2)设g(x)=xf(x),h(x)=2ax2-(2a-1)x+a-1,若x≥1时,g(x)≤h(x)恒成立,求实数a的取值范围.
分析 (1)求出函数的导数,解关于导函数的不等式,求出函数的单调区间,从而求出函数的最大值即可;
(2)当x≥1时,g(x)≤h(x)恒成立,即为xlnx-ax2+(2a-1)x≤a-1,讨论x=1和x>1,由参数分离和构造函数g(x)=xlnx-(x-1)-(x-1)2(x>1),求出导数和单调性,即可判断g(x)的单调性,可得a的范围.
解答 解:(1)a=-1时,f(x)=-x+lnx,f′(x)=-1+$\frac{1}{x}$,
令f′(x)>0,解得:0<x<1,令f′(x)<0,解得:x>1,
故f(x)在(0,1)递增,在(1,+∞)递减,
故f(x)max=f(1)=-1;
(2)当x≥1时,g(x)≤h(x)恒成立,
即为xlnx-ax2+(2a-1)x≤a-1,
当x=1时,上式显然成立.
当x>1时,可得a≥$\frac{xlnx-x+1}{{(x-1)}^{2}}$,
由 $\frac{xlnx-x+1}{{(x-1)}^{2}}$-1=$\frac{xlnx-(x-1){-(x-1)}^{2}}{{(x-1)}^{2}}$,
设g(x)=xlnx-(x-1)-(x-1)2(x>1),
g′(x)=1+lnx-1-2(x-1)=lnx-2(x-1),
由g″(x)=$\frac{1}{x}$-2<0在x>1恒成立,
可得g′(x)在(1,+∞)递减,可得g′(x)<g′(1)=0,
即g(x)在(1,+∞)递减,可得g(x)<g(1)=0,
则 $\frac{xlnx-x+1}{{(x-1)}^{2}}$<1成立,
即有a≥1.
即a的范围是[1,+∞).
点评 本题考查导数的运用:求单调区间和极值、最值,考查不等式成立问题的解法,注意运用参数分离和构造函数法,求得导数判断单调性,考查化简整理的运算能力,属于中档题.

| 不喜欢戏剧 | 喜欢戏剧 | |
| 男性青年观众 | 40 | 10 |
| 女性青年观众 | 40 | 60 |
| A. | $\frac{16π}{3}$ | B. | $\frac{40π}{3}$ | C. | $\frac{64π}{3}$ | D. | $\frac{80π}{3}$ |
| A. | 98 | B. | 49 | C. | 14 | D. | 147 |
| A. | {-2}∪[2,+∞) | B. | (-∞,-2)∪[2,+∞) | C. | [2,+∞) | D. | {0}∪[2,+∞) |
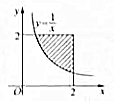 在平面直角坐标系内任取一个点P(x,y)满足$\left\{\begin{array}{l}{0≤x≤2}\\{0≤y≤2}\end{array}\right.$,则点P落在曲线y=$\frac{1}{x}$与直线x=2,y=2围成的阴影区域(如图所示)内的概率为$\frac{3-ln4}{4}$.
在平面直角坐标系内任取一个点P(x,y)满足$\left\{\begin{array}{l}{0≤x≤2}\\{0≤y≤2}\end{array}\right.$,则点P落在曲线y=$\frac{1}{x}$与直线x=2,y=2围成的阴影区域(如图所示)内的概率为$\frac{3-ln4}{4}$.