题目内容
17.已知三棱锥P-ABC的四个顶点均在某球面上,PC为该球的直径,△ABC是边长为4的等边三角形,三棱椎P-ABC的体积为$\frac{16}{3}$,则该三棱锥的外接球的表面积为( )| A. | $\frac{16π}{3}$ | B. | $\frac{40π}{3}$ | C. | $\frac{64π}{3}$ | D. | $\frac{80π}{3}$ |
分析 根据题意作出图形,欲求球O的表面积,只须求球的半径r.利用截面圆的性质即可求出OO1,进而求出底面ABC上的高PD,即可计算出三棱锥的体积,从而建立关于r的方程,即可求出r,从而解决问题.
解答 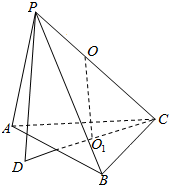 解:根据题意作出图形
解:根据题意作出图形
设球心为O,球的半径r.过ABC三点的小圆的圆心为O1,
则OO1⊥平面ABC,延长CO1交球于点D,则PD⊥平面ABC.
∵CO1=$\frac{4\sqrt{3}}{3}$,
∴OO1=$\sqrt{{r}^{2}-\frac{16}{3}}$,
∴高PD=2OO1=2$\sqrt{{r}^{2}-\frac{16}{3}}$,
∵△ABC是边长为4正三角形,
∴S△ABC=$\frac{\sqrt{3}}{4}×{4}^{2}$=4$\sqrt{3}$
∴V三棱锥P-ABC=$\frac{1}{3}$×4$\sqrt{3}$×2$\sqrt{{r}^{2}-\frac{16}{3}}$=$\frac{16}{3}$
∴r2=$\frac{20}{3}$.
则球O的表面积为4πr2=$\frac{80π}{3}$
故选:D.
点评 本题考查棱锥的体积,考查球内接多面体,解题的关键是确定点P到面ABC的距离.

练习册系列答案
相关题目
8.已知向量$\overrightarrow{a}$,$\overrightarrow{b}$满足|$\overrightarrow{a}$|=2,|$\overrightarrow{b}$|=3,($\overrightarrow{a}$-$\overrightarrow{b}$)•$\overrightarrow{a}$=1,则$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
5.某单位为制定节能减排的计划,随机统计了某4天的用电量y(单位:度)与当天气温x(单位:°C),并制作了对照表(如表),由表中数据,得线性回归方程$\hat y=-2x+a$,当某天的气温为-5°C时,预测当天的用电量约为( )
| x | 18 | 13 | 10 | -1 |
| y | 24 | 34 | 38 | 64 |
| A. | 65度 | B. | 68度 | C. | 70度 | D. | 72度 |
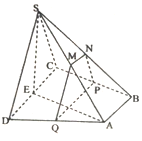 如图,四棱锥S-ABCD中,底面ABCD为直角梯形,AB∥CD,BC⊥CD,平面SCD⊥平面ABCD,SC=SD=CD=AD=2AB=2,M,N分别为SA,SB的中点,E为CD中点,过M,N作平面MNPQ分别于BC,AD交于点P,Q,若|DQ|=λ|DA|
如图,四棱锥S-ABCD中,底面ABCD为直角梯形,AB∥CD,BC⊥CD,平面SCD⊥平面ABCD,SC=SD=CD=AD=2AB=2,M,N分别为SA,SB的中点,E为CD中点,过M,N作平面MNPQ分别于BC,AD交于点P,Q,若|DQ|=λ|DA|