题目内容
1.一已知等差数列{an}中,其前n项和为Sn,若a3+a4+a5=42,则S7=( )| A. | 98 | B. | 49 | C. | 14 | D. | 147 |
分析 根据题意和等差数列的性质求出a4的值,由等差数列的前n项和公式求出S7的值.
解答 解:等差数列{an}中,因为a3+a4+a5=42,
所以3a4=42,解得a4=14,
所以S7=$\frac{7({a}_{1}+{a}_{7})}{2}$=7a4=7×14=98,
故选A.
点评 本题考查等差数列的性质、前n项和公式的灵活应用,属于基础题.

练习册系列答案
相关题目
13.设x∈R,若“|x-a|<1(a∈R)”是“x2+x-2>0”的充分不必要条件,则a的取值范围是( )
| A. | (-∞,-3]∪[2,+∞) | B. | (-∞,-3)∪(2,+∞) | C. | (-3,2) | D. | [-3,2] |
8.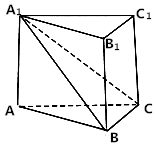 如图所示,在直三棱柱ABC-A1B1C1中,平面A1BC⊥侧面A1ABB1,且AA1=AB=2.
如图所示,在直三棱柱ABC-A1B1C1中,平面A1BC⊥侧面A1ABB1,且AA1=AB=2.
(1)求证:AB⊥BC;
(2)若∠CAB=$\frac{π}{6}$,求三棱锥B1-A1BC的体积.
 如图所示,在直三棱柱ABC-A1B1C1中,平面A1BC⊥侧面A1ABB1,且AA1=AB=2.
如图所示,在直三棱柱ABC-A1B1C1中,平面A1BC⊥侧面A1ABB1,且AA1=AB=2.(1)求证:AB⊥BC;
(2)若∠CAB=$\frac{π}{6}$,求三棱锥B1-A1BC的体积.
9.已知等比数列{an}的前n项和为Sn,a1+a3=30,S4=120,设bn=1+log3an,那么数列{bn}的前15项和为( )
| A. | 152 | B. | 135 | C. | 80 | D. | 16 |
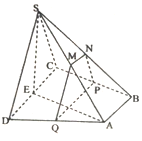 如图,四棱锥S-ABCD中,底面ABCD为直角梯形,AB∥CD,BC⊥CD,平面SCD⊥平面ABCD,SC=SD=CD=AD=2AB=2,M,N分别为SA,SB的中点,E为CD中点,过M,N作平面MNPQ分别于BC,AD交于点P,Q,若|DQ|=λ|DA|
如图,四棱锥S-ABCD中,底面ABCD为直角梯形,AB∥CD,BC⊥CD,平面SCD⊥平面ABCD,SC=SD=CD=AD=2AB=2,M,N分别为SA,SB的中点,E为CD中点,过M,N作平面MNPQ分别于BC,AD交于点P,Q,若|DQ|=λ|DA|