题目内容
4．已知等比数列{an}中，a1+a3=$\frac{5}{2}，{a_2}+{a_4}=\frac{5}{4}$，则a6=$\frac{1}{16}$．分析 根据条件列出关于a1和q的方程组，解得即可．
解答 解：∵a1+a3=$\frac{5}{2}，{a_2}+{a_4}=\frac{5}{4}$，
∴$\left\{\begin{array}{l}{{a}_{1}+{a}_{1}{q}^{2}=\frac{5}{2}}\\{{a}_{1}q+{a}_{1}{q}^{3}=\frac{5}{4}}\end{array}\right.$，
解得q=$\frac{1}{2}$，a1=2，
∴a6=2×（$\frac{1}{2}$）5=$\frac{1}{16}$，
故答案为：$\frac{1}{16}$
点评 本题考查等比数列的定义，是基础题，解题时要认真审题，注意等比数列的性质的合理运用．
练习册系列答案
相关题目
14．已知棱长为$\sqrt{6}$的正四面体ABCD（四个面都是正三角形），在侧棱AB上任取一点P（与A，B都不重合），若点P到平面BCD及平面ACD的距离分别为a，b，则$\frac{4}{a}$+$\frac{1}{b}$的最小值为（ ）
| A． | $\frac{7}{2}$ | B． | 4 | C． | $\frac{9}{2}$ | D． | 5 |
19．
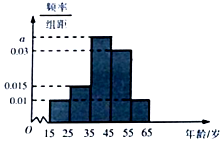2017年郴州市两会召开前夕，某网站推出两会热点大型调查，调查数据表明，民生问题是百姓最为关心的热点，参与调查者中关注此问题的约占80%，现从参与者中随机选出200人，并将这200人按年龄分组：第1组[15，25），第2组[25，35），第3组[35，45），第4组[45，55），第5组[55，65），得到的频率分布直方图如图所示：
（Ⅰ）求出频率分布直方图中a的值，并求出这200人的平均年龄；
（Ⅱ）现在要从年龄较小的第1组和第2组中用分层抽样的方法抽取5人，再从这5人中随机抽取2人赠送礼品，求抽取的2人中至少有人年龄在第1组的概率；
（Ⅲ）把年龄在第1，2，3组的居民称为青少年组，年龄在第4，5组的居民称为中老年组，若选出的200人中不关注民生问题的人中老年人有10人，根据以上数据，完成以下列联表，并判断是否可以在犯错误概率不超过1%的前提下，认为关注民生问题与年龄有关？
附：
${K^2}=\frac{{n{{（ad-bc）}^2}}}{（a+b）（c+d）（a+c）（b+d）}$，其中n=a+b+c+d．
2017年郴州市两会召开前夕，某网站推出两会热点大型调查，调查数据表明，民生问题是百姓最为关心的热点，参与调查者中关注此问题的约占80%，现从参与者中随机选出200人，并将这200人按年龄分组：第1组[15，25），第2组[25，35），第3组[35，45），第4组[45，55），第5组[55，65），得到的频率分布直方图如图所示：（Ⅰ）求出频率分布直方图中a的值，并求出这200人的平均年龄；
（Ⅱ）现在要从年龄较小的第1组和第2组中用分层抽样的方法抽取5人，再从这5人中随机抽取2人赠送礼品，求抽取的2人中至少有人年龄在第1组的概率；
（Ⅲ）把年龄在第1，2，3组的居民称为青少年组，年龄在第4，5组的居民称为中老年组，若选出的200人中不关注民生问题的人中老年人有10人，根据以上数据，完成以下列联表，并判断是否可以在犯错误概率不超过1%的前提下，认为关注民生问题与年龄有关？
| 关注民生 | 不关注民生 | 合计 | |
| 青少年组 | 90 | 30 | 120 |
| 中老年组 | 70 | 10 | 80 |
| 合计 | 160 | 40 | 200 |
| p（K2≥k0） | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
13．设x∈R，若“|x-a|＜1（a∈R）”是“x2+x-2＞0”的充分不必要条件，则a的取值范围是（ ）
| A． | （-∞，-3]∪[2，+∞） | B． | （-∞，-3）∪（2，+∞） | C． | （-3，2） | D． | [-3，2] |
12．一汽车厂生产A，B，C三类轿车，每类轿车均有舒适型和标准型两种型号，某月的产量如表（单位：辆）：
按分层抽样的方法在这个月生产的A，B，C三类轿车中抽取50辆，其中有A类轿车10辆．
（Ⅰ）求z的值；
（Ⅱ）分别求从B，C类轿车中抽取的车辆数．
| 轿车A | 轿车B | 轿车C | |
| 舒适型 | 100 | 150 | z |
| 标准型 | 300 | 450 | 600 |
（Ⅰ）求z的值；
（Ⅱ）分别求从B，C类轿车中抽取的车辆数．