题目内容
已知二次函数f(x)满足f(x+1)-f(x)=2x,且f(0)=1.
(1)求f(x)的解析式.
(2)画出函数的图象.
(3)根据图象求函数在区间[-1,2]上的最大值.
(1)求f(x)的解析式.
(2)画出函数的图象.
(3)根据图象求函数在区间[-1,2]上的最大值.
考点:二次函数的性质
专题:综合题,函数的性质及应用
分析:(1)设f(x)=ax2+bx+c,利用f(x+1)-f(x)=2x,且f(0)=1,求出a,b,c,即可求f(x)的解析式.
(2)确定对称轴、顶点,可得函数的图象.
(3)根据图象求函数在区间[-1,2]上的最大值.
(2)确定对称轴、顶点,可得函数的图象.
(3)根据图象求函数在区间[-1,2]上的最大值.
解答:
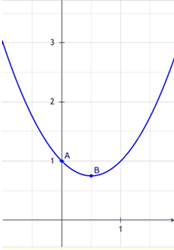 解:(1)设f(x)=ax2+bx+c,由f(0)=1得c=1,故f(x)=ax2+bx+1.---------(2分)
解:(1)设f(x)=ax2+bx+c,由f(0)=1得c=1,故f(x)=ax2+bx+1.---------(2分)
∵f(x+1)-f(x)=2x,
∴a(x+1)2+b(x+1)+1-(ax2+bx+1)=2x.------------------------(4分)
即2ax+a+b=2x,所以
,∴
,∴f(x)=x2-x+1.-------------(6分)
(2)图象如图---------------------------------(9分)
(3)由图象得函数在[-1,2]的最大值是3--------------------(12分)
 解:(1)设f(x)=ax2+bx+c,由f(0)=1得c=1,故f(x)=ax2+bx+1.---------(2分)
解:(1)设f(x)=ax2+bx+c,由f(0)=1得c=1,故f(x)=ax2+bx+1.---------(2分)∵f(x+1)-f(x)=2x,
∴a(x+1)2+b(x+1)+1-(ax2+bx+1)=2x.------------------------(4分)
即2ax+a+b=2x,所以
|
|
(2)图象如图---------------------------------(9分)
(3)由图象得函数在[-1,2]的最大值是3--------------------(12分)
点评:本题考查函数的解析式,考查二次函数的性质,考查学生分析解决问题的能力,比较基础.

练习册系列答案
相关题目
不等式|5x-x2|<6的解集为( )
| A、{x|x<2或x>3} |
| B、{x|-1<x<2或3<x<6} |
| C、{x|-1<x<6} |
| D、{x|2<x<3} |
两个非零向量
,
垂直的充要条件是( )
| a |
| b |
A、|
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、(
|
已知命题p:实数x满足logax>loga(2-x),其中0<a<1,则使命题p成立的必要不充分条件是( )
| A、1<x<2 | ||
| B、0<x<1 | ||
| C、-1<x<1 | ||
D、
|