题目内容
20.在直角坐标xOy中,直线l的参数方程为{$\left\{\begin{array}{l}{x=\frac{\sqrt{2}}{2}t}\\{y=3+\frac{\sqrt{2}}{2}t}\end{array}\right.$(t为参数)在以O为极点.x轴正半轴为极轴的极坐标系中.曲线C的极坐标方程为ρ=4sinθ-2cosθ.(I)求直线l的普通方程与曲线C的直角坐标方程:
(Ⅱ)若直线l与y轴的交点为P,直线l与曲线C的交点为A,B,求|PA||PB|的值.
分析 (1)由x=$\frac{\sqrt{2}}{2}$t,得t=$\sqrt{2}$x,将其代入y=3+$\frac{\sqrt{2}}{2}$t中,即可得出直线l的直角坐标方程.由ρ=2cosθ+4sinθ,得ρ2=2ρcosθ+4ρsinθ,把$\left\{\begin{array}{l}{x=ρcosθ}\\{y=ρsinθ}\end{array}\right.$代入即可得出曲线C的直角坐标方程.
(2)分别求出P、A、B的坐标,根据两点之间的距离公式计算即可.
解答 解:(1)由x=$\frac{\sqrt{2}}{2}$t,得t=$\sqrt{2}$x,将其代入y=3+$\frac{\sqrt{2}}{2}$t中得:y=x+3,
∴直线l的直角坐标方程为x-y+3=0.
由ρ=4sinθ-2cosθ,得ρ2=4ρsinθ-2ρcosθ,
∴x2+y2=4y-2x,即x2+y2+2x-4y=0,
∴曲线C的直角坐标方程为x2+y2+2x-4y=0;
(2)由l:y=x+3,得P(0,3),
由$\left\{\begin{array}{l}{y=x+3}\\{{x}^{2}{+y}^{2}+2x-4y=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=-\frac{2+\sqrt{10}}{2}}\\{y=\frac{4-\sqrt{10}}{2}}\end{array}\right.$或$\left\{\begin{array}{l}{x=\frac{-2+\sqrt{10}}{2}}\\{y=\frac{4+\sqrt{10}}{2}}\end{array}\right.$,
∴|PA||PB|=$\sqrt{{(-\frac{2+\sqrt{10}}{2}-0)}^{2}{+(\frac{4-\sqrt{10}}{2}-3)}^{2}}$•$\sqrt{{(\frac{-2+\sqrt{10}}{2}-0)}^{2}{+(\frac{4+\sqrt{10}}{2}-3)}^{2}}$=3.
点评 本题考查了参数方程化为普通方程、极坐标方程化为直角坐标方程、曲线的交点,考查了推理能力与计算能力,属于中档题.

 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案| A. | 2 | B. | $\frac{3}{2}$ | C. | $\frac{1}{11}$ | D. | $\frac{1}{2}$ |
| A. |  | B. |  | C. |  | D. | D |
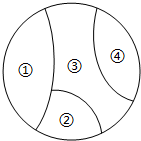 将某城市分成如图所示的4个区,需要绘制一幅城市分区地图,有红、黄、蓝、绿、紫5种不同的颜色,图中①、②、③、④每区只涂一色,且相邻两区必须涂不同颜色,则涂色时恰好用了3种不同颜色的概率是( )
将某城市分成如图所示的4个区,需要绘制一幅城市分区地图,有红、黄、蓝、绿、紫5种不同的颜色,图中①、②、③、④每区只涂一色,且相邻两区必须涂不同颜色,则涂色时恰好用了3种不同颜色的概率是( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{5}$ |
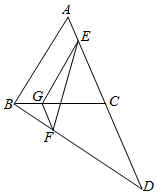 如图,AB、CD是两条异面直线,AB=CD=3,E、F分别是AC、BD上的点,且AE:EC=BF:DF=1:2,EF=$\sqrt{7}$,求AB和CD所成角的大小.
如图,AB、CD是两条异面直线,AB=CD=3,E、F分别是AC、BD上的点,且AE:EC=BF:DF=1:2,EF=$\sqrt{7}$,求AB和CD所成角的大小.