题目内容
8.已知定义域为R的奇函数f(x)满足f(x)+f(2-x)=0,且当x∈[-1,0)时,f(x)=-$\sqrt{1-{x}^{2}}$,函数g(x)为偶函数,且当x≥0时,g(x)=$\sqrt{x}$,则方程g(x)-f(x)=1区间[-3,3]上的解的个数为( )| A. | 2 | B. | 3 | C. | 4 | D. | 6 |
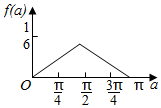
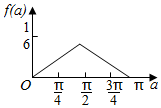
分析 确定f(x)的周期为2,作出y=f(x)与y=g(x)-1(0,3]的图象,即可得出结论.
解答  解:∵定义域为R的奇函数f(x)满足f(x)+f(2-x)=0,
解:∵定义域为R的奇函数f(x)满足f(x)+f(2-x)=0,
∴f(-x+2)=f(-x),
∴f(x)的周期为2,
作出y=f(x)与y=g(x)-1(0,3]的图象,如图所示,有两个交点,方程g(x)-f(x)=1区间[-3,0]上的解的个数为1,
则方程g(x)-f(x)=1区间[-3,3]上的解的个数为3.
故选:B.
点评 本题考查函数的图象与性质,考查函数的周期性,正确作出函数的图象是关键.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
16.已知一组数据2(x1-1),2(x2-1),…,2(x2015-1)的平均数为6,标准差为4,则新数据x1,x2,…,x2015的平均数与标准差分别为( )
| A. | 4,1 | B. | 3,2 | C. | 4,2 | D. | 3,1 |
18.设函数f(x)=-x2+2x+3,x∈(-3,2],则f(x)的值域为( )
| A. | (-12,3] | B. | (-12,3) | C. | (-12,4] | D. | (-12,4) |
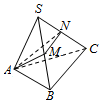 如图,一个三棱锥,底面ABC为正三角形,侧棱SA=SB=SC=1,∠ASB=30°,M、N分别为棱SB和SC上的点,求△AMN的周长的最小值.
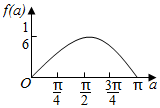
如图,一个三棱锥,底面ABC为正三角形,侧棱SA=SB=SC=1,∠ASB=30°,M、N分别为棱SB和SC上的点,求△AMN的周长的最小值.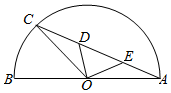 如图,$\widehat{AB}$为半圆,O为圆心,OA=1,C为$\widehat{AB}$上的动点,D、E为线段AC的三等分点,设∠AOC=α,将△ODE的面积为y=f(α),则y=f(α)的图象大致为( )
如图,$\widehat{AB}$为半圆,O为圆心,OA=1,C为$\widehat{AB}$上的动点,D、E为线段AC的三等分点,设∠AOC=α,将△ODE的面积为y=f(α),则y=f(α)的图象大致为( )