题目内容
15．已知m为非零常数，对x∈R，有f（x+m）=$\frac{1+f（x）}{1-f（x）}$恒成立，则函数f（x）的最小正周期是4m．分析 根据题意分别令x取“x+m”、“x+2m”代入式子化简，由周期的定义可求出函数的最小正周期．
解答 解：因为对x∈R，有f（x+m）=$\frac{1+f（x）}{1-f（x）}$恒成立，
所以f（x+2m）=$\frac{1+f（x+m）}{1-f（x+m）}$=$\frac{1+\frac{1+f（x）}{1-f（x）}}{1-\frac{1+f（x）}{1-f（x）}}$=-$\frac{1}{f（x）}$，
则f（x+4m）=-$\frac{1}{f（x+2m）}$=-$\frac{1}{-\frac{1}{f（x）}}$=f（x），
则f（x）的周期是4m，
故答案为：4m．
点评 本题考查函数周期的定义，以及赋值法的应用，考查化简、变形能力，属于中档题．
练习册系列答案
相关题目
5．已知a，b是两条直线，α是一个平面，则下列判断正确的是（ ）
| A． | a⊥α，b⊥α，则a⊥b | B． | a∥α，b?α，则a∥b | ||
| C． | a⊥b，b?α，则a⊥α | D． | a∥α，b?α，a?α，则a∥α |
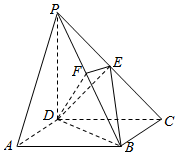如图，在四棱锥P-ABCD中，底面ABCD是矩形，侧棱PD⊥底面ABCD，PD=DC，点E是PC的中点，作EF⊥PB交PB于点F．
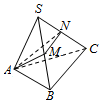如图，一个三棱锥，底面ABC为正三角形，侧棱SA=SB=SC=1，∠ASB=30°，M、N分别为棱SB和SC上的点，求△AMN的周长的最小值．
在空间四边形ABCD中，E、F、O、H分别是AB、BC、CD、DA的中点，且AC=BD，求证：EO与FH互相垂直平分．