题目内容
5．
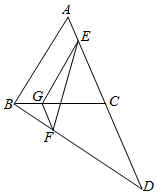如图，AB、CD是两条异面直线，AB=CD=3，E、F分别是AC、BD上的点，且AE：EC=BF：DF=1：2，EF=$\sqrt{7}$，求AB和CD所成角的大小．
分析 连结BD，在BD上取点G，使BG：GD=1：2，连结GF，则∠EGF即AB与CD所成的角，由此能求出AB与CD所成的角的大小．
解答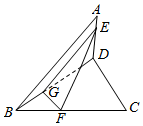 
解：如图，连结BD，在BD上取点G，
使BG：GD=1：2，连结GF．
∵AB、CD是两条异面直线，AB=CD=3，
E、F分别是AC、BD上的点，且AE：EC=BF：DF=1：2，
∴EG∥AB，GF∥CD．
∴∠EGF即AB与CD所成的角，
在AEGF中，由已知，得：EG=2，FG=1，而EF=$\sqrt{7}$，
由余弦定理得cos∠EGF=-$\frac{1}{2}$，
∴∠EGF=120°，
∴AB与CD所成的角为60°．
点评 本题考查异面直线所成角的大小的求法，是基础题，解题时要认真审题，注意空间思维能力的培养．
练习册系列答案
相关题目
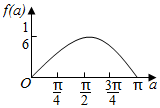
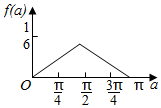
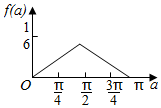
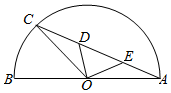如图，$\widehat{AB}$为半圆，O为圆心，OA=1，C为$\widehat{AB}$上的动点，D、E为线段AC的三等分点，设∠AOC=α，将△ODE的面积为y=f（α），则y=f（α）的图象大致为（ ）
