题目内容
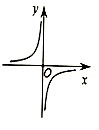
1. 设k是一个正整数,(1+$\frac{x}{k}$)k的展开式中第四项的系数为$\frac{1}{16}$,任取x∈[0,4],y∈[0,16],如图,则点(x,y)恰好落在函数y=x2与y=kx的图象所围成的阴影区域内的概率为( )
设k是一个正整数,(1+$\frac{x}{k}$)k的展开式中第四项的系数为$\frac{1}{16}$,任取x∈[0,4],y∈[0,16],如图,则点(x,y)恰好落在函数y=x2与y=kx的图象所围成的阴影区域内的概率为( )| A. | $\frac{17}{96}$ | B. | $\frac{5}{32}$ | C. | $\frac{1}{6}$ | D. | $\frac{7}{48}$ |
分析 先利用二项式定理求出k的值,再利用积分求阴影部分的面积,积分的上下限由方程组求得,然后利用几何概型的概率公式解答.
解答 解:根据题意得${C}_{k}^{3}$•${(\frac{1}{k})}^{3}$=$\frac{1}{16}$,整理得5k2-24k+16=0,
解得k=4或k=$\frac{4}{5}$(不是整数,舍去);
解方程组$\left\{\begin{array}{l}{y{=x}^{2}}\\{y=4x}\end{array}\right.$,
解得x=0或x=4;
∴阴影部分的面积为:
S′=${∫}_{0}^{4}$(4x-x2)dx=(2x2-$\frac{1}{3}$x3)${|}_{0}^{4}$=2×42-$\frac{1}{3}$×43=$\frac{32}{3}$,
任取x∈[0,4],y∈[0,16],则点(x,y)对应区域面积为:
S=4×16=64,
由几何概型概率求法得点(x,y)恰好落在阴影区域内的概率为:
P=$\frac{S′}{S}$=$\frac{\frac{32}{3}}{64}$=$\frac{1}{6}$;
故选:C.
点评 本题主要考查了定积分、二项式定理和几何概型的概率计算问题,应用定积分求平面图形面积时,积分变量的选取至关重要,是综合题.

练习册系列答案
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案
相关题目
12. 某保险公司有款保险产品的历史收益率(收益率=利润÷保费收入)的频率分布直方图如图所示:
某保险公司有款保险产品的历史收益率(收益率=利润÷保费收入)的频率分布直方图如图所示:
(1)试估计这款保险产品的收益率的平均值;
(Ⅱ)设每份保单的保费在20元的基础上每增加x元,对应的销量y(万份),从历史销售记录中抽样得到如下5组x与y的对应数据:
由上表,知x与y有较强的线性相关关系,且据此计算出的回归方程为$\widehat{y}$=10.0-bx.
(i)求参数b的估计值;
(ii)若把回归方程$\widehat{y}$=10.0-bx当作y与x的线性关系,用(Ⅰ)中求出的收益率的平均值作为此产品的收益率,试问每份保单的保费定为多少元时此产品可获得最大利润,并求出该最大利润.注:保险产品的保费收入=每份保单的保费×销量.
 某保险公司有款保险产品的历史收益率(收益率=利润÷保费收入)的频率分布直方图如图所示:
某保险公司有款保险产品的历史收益率(收益率=利润÷保费收入)的频率分布直方图如图所示:(1)试估计这款保险产品的收益率的平均值;
(Ⅱ)设每份保单的保费在20元的基础上每增加x元,对应的销量y(万份),从历史销售记录中抽样得到如下5组x与y的对应数据:
| X(元) | 25 | 30 | 38 | 45 | 52 |
| 销售量y(万份) | 7.5 | 7.1 | 6.0 | 5.6 | 4.8 |
(i)求参数b的估计值;
(ii)若把回归方程$\widehat{y}$=10.0-bx当作y与x的线性关系,用(Ⅰ)中求出的收益率的平均值作为此产品的收益率,试问每份保单的保费定为多少元时此产品可获得最大利润,并求出该最大利润.注:保险产品的保费收入=每份保单的保费×销量.
6. 我州某高中从高二年级甲、乙两个班种各选出7名学生参加2017年全国高中数学联赛(四川初赛),他们取得的成绩(满分140分)的茎叶图如图所示,其中甲班学生成绩的中位数是81,乙班学生成绩的平均数是86,若正实数a、b满足:a,G,b成等差数列且x,G,y成等比数列,则$\frac{1}{a}$+$\frac{4}{b}$的最小值为( )
我州某高中从高二年级甲、乙两个班种各选出7名学生参加2017年全国高中数学联赛(四川初赛),他们取得的成绩(满分140分)的茎叶图如图所示,其中甲班学生成绩的中位数是81,乙班学生成绩的平均数是86,若正实数a、b满足:a,G,b成等差数列且x,G,y成等比数列,则$\frac{1}{a}$+$\frac{4}{b}$的最小值为( )
 我州某高中从高二年级甲、乙两个班种各选出7名学生参加2017年全国高中数学联赛(四川初赛),他们取得的成绩(满分140分)的茎叶图如图所示,其中甲班学生成绩的中位数是81,乙班学生成绩的平均数是86,若正实数a、b满足:a,G,b成等差数列且x,G,y成等比数列,则$\frac{1}{a}$+$\frac{4}{b}$的最小值为( )
我州某高中从高二年级甲、乙两个班种各选出7名学生参加2017年全国高中数学联赛(四川初赛),他们取得的成绩(满分140分)的茎叶图如图所示,其中甲班学生成绩的中位数是81,乙班学生成绩的平均数是86,若正实数a、b满足:a,G,b成等差数列且x,G,y成等比数列,则$\frac{1}{a}$+$\frac{4}{b}$的最小值为( )| A. | $\frac{4}{9}$ | B. | 2 | C. | $\frac{9}{4}$ | D. | 8 |
5.数列{an+1}是各项均正的等比数列,a1=1,a3=13-2a2则数列{an}的前n项和Sn为( )
| A. | Sn=2n-2 | B. | Sn=2n+1-2-n | C. | Sn=2n-1-n | D. | Sn=2n-1 |
3.在新媒体时代,酒香也怕巷子深,宣传是让大众最快了解自己产品的最有效的手段,已知某种产品的宣传费用x与销售总额y的统计数据如下表所示:
根据上表求得的回归方程$\widehat{y}$=9.4x+$\widehat{a}$,据此模型预测宣传费用为6万元时销售额为( )
| 宣传费用x万元 | 2 | 3 | 4 | 5 |
| 销售总额y万元 | 26 | 39 | 49 | 54 |
| A. | 63.6万元 | B. | 65.5万元 | C. | 67.7万元 | D. | 72.0万元 |