题目内容
9.如图是函数y=f(x)的导函数y=f′(x)的图象,那么函数y=f(x)的图象最有可能是( )
| A. |  | B. |  | C. |  | D. | 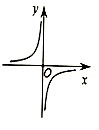 |
分析 根据题意,由导函数的图象分析可得当x∈(-∞,0)时,函数f(x)为减函数,当x∈(0,+∞)时,函数f(x)为增函数;据此分析选项即可得答案.
解答 解:根据题意,由函数y=f(x)的导函数y=f′(x)的图象分析可得:
当x∈(-∞,0)时,f′(x)<0恒成立,函数f(x)为减函数;
当x∈(0,+∞)时,f′(x)>0恒成立,函数f(x)为增函数;
据此依次分析选项可得C符合;
故选:C.
点评 本题考查函数的导数与单调性的关系,涉及函数的图象,关键是掌握函数导数的符号与函数单调性的关系.

练习册系列答案
相关题目
20.定积分${∫}_{0}^{3}$$\sqrt{9-{x}^{2}}$dx的值是( )
| A. | 9π | B. | $\frac{9π}{2}$ | C. | $\frac{9}{4}$π | D. | $\frac{9}{8}$π |
17.已知平面向量$\overrightarrow{a},\overrightarrow{b}$满足$\overrightarrow{a}$=(1,2),|$\overrightarrow{b}$|=$\sqrt{10}$,且|2$\overrightarrow{a}$+$\overrightarrow{b}$|=$\sqrt{14}$|,则向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角的余弦值为( )
| A. | -$\frac{2\sqrt{2}}{5}$ | B. | -$\frac{3\sqrt{2}}{5}$ | C. | $\frac{2\sqrt{2}}{5}$ | D. | $\frac{3\sqrt{2}}{5}$ |
14.设函数f(θ)=$\sqrt{3}$sinθ+cosθ,其中角θ的顶点与坐标原点重合,始边与x轴非负半轴重合,终边经过点P($\frac{1}{2}$,$\frac{{\sqrt{3}}}{2}$),则f(θ)=( )
| A. | 2 | B. | $\sqrt{3}$ | C. | 1 | D. | $\frac{\sqrt{3}}{2}$ |
1. 设k是一个正整数,(1+$\frac{x}{k}$)k的展开式中第四项的系数为$\frac{1}{16}$,任取x∈[0,4],y∈[0,16],如图,则点(x,y)恰好落在函数y=x2与y=kx的图象所围成的阴影区域内的概率为( )
设k是一个正整数,(1+$\frac{x}{k}$)k的展开式中第四项的系数为$\frac{1}{16}$,任取x∈[0,4],y∈[0,16],如图,则点(x,y)恰好落在函数y=x2与y=kx的图象所围成的阴影区域内的概率为( )
 设k是一个正整数,(1+$\frac{x}{k}$)k的展开式中第四项的系数为$\frac{1}{16}$,任取x∈[0,4],y∈[0,16],如图,则点(x,y)恰好落在函数y=x2与y=kx的图象所围成的阴影区域内的概率为( )
设k是一个正整数,(1+$\frac{x}{k}$)k的展开式中第四项的系数为$\frac{1}{16}$,任取x∈[0,4],y∈[0,16],如图,则点(x,y)恰好落在函数y=x2与y=kx的图象所围成的阴影区域内的概率为( )| A. | $\frac{17}{96}$ | B. | $\frac{5}{32}$ | C. | $\frac{1}{6}$ | D. | $\frac{7}{48}$ |
11.某企业生产A、B两种产品,生产 1t产品所消耗的煤和电及所获利润如表:
又知两种产品的生产量不少于10t.该企业用电不超过360kw.h,用煤不超过240t,问生产A、B两种产品各多少吨时,才能获得最大的利润?最大的利润是多少?
| 产品 | 所需能源 | 利润(万元) | |
| 煤(t) | 电(kw•h) | ||
| A | 6 | 6 | 9 |
| B | 4 | 9 | 1 2 |