题目内容
已知函数f（x）=sin（ωx+φ）（其中ω＞0|φ|＜
）图象相邻对称轴的距离为
，一个对称中心为（-
，0），为了得到g（x）=cosωx的图象，则只要将f（x）的图象（ ）
| π |
| 2 |
| π |
| 2 |
| π |
| 6 |
A、向右平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向左平移
|
考点：函数y=Asin（ωx+φ）的图象变换
专题：三角函数的图像与性质
分析：由周期求得ω，根据图象的对称中心求得φ的值，可得函数的解析式，再根据函数y=Asin（ωx+φ）的图象变换规律得出结论．
解答：
解：由题意可得函数的最小正周期为
=2×
，∴ω=2．
再根据-
×2+φ=kπ，|φ|＜
，k∈z，可得φ=
，f（x）=sin（2x+
），
故将f（x）的图象向左平移
个单位，可得y=sin[2（x+
）+
]=sin（2x+
）=cos2x的图象，
故选：D．
| 2π |
| ω |
| π |
| 2 |
再根据-
| π |
| 6 |
| π |
| 2 |
| π |
| 3 |
| π |
| 3 |
故将f（x）的图象向左平移
| π |
| 12 |
| π |
| 12 |
| π |
| 3 |
| π |
| 2 |
故选：D．
点评：本题主要考查由函数y=Asin（ωx+φ）的部分图象求解析式，诱导公式的应用，函数y=Asin（ωx+φ）的图象变换规律，属于基础题．
练习册系列答案
相关题目
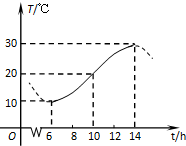如图，某地一天中6时至14时的温度变化曲线近似满足函数y=Asin（ωx+φ）+b（其中ω＞0，| π |
| 2 |
| A、30℃ | B、27℃ |
| C、25℃ | D、24℃ |
设数列{an}是公比为q的等比数列，则“0＜q＜1”是“{an}为递减数列”的（ ）
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
下列四个函数中，与y=x表示同一函数的是（ ）
A、y=
| |||
B、y=
| |||
C、y=(
| |||
D、y=
|