题目内容
设函数F(x)=f(x)-ag(x)(a为常数),f(x)=
,g(x)=
+lnx,(e是自然对数的底数,e=2.71828…).
(Ⅰ)求曲线y=g(x)在点(1,g(1))处的切线方程;
(Ⅱ)当a≤0时,求函数F(x)的最大值和最小值;
(Ⅲ)若函数F(x)在(0,2)内存在两个极值点,求a的取值范围.
| ex |
| x2 |
| 2 |
| x |
(Ⅰ)求曲线y=g(x)在点(1,g(1))处的切线方程;
(Ⅱ)当a≤0时,求函数F(x)的最大值和最小值;
(Ⅲ)若函数F(x)在(0,2)内存在两个极值点,求a的取值范围.
考点:利用导数研究曲线上某点切线方程,利用导数求闭区间上函数的最值
专题:导数的综合应用
分析:(Ⅰ)求出函数g(x)的导函数,得到函数在x=1时的导数,再求出g(1)的值,由直线方程的点斜式求得曲线y=g(x)在点(1,g(1))处的切线方程;
(Ⅱ)求出函数F(x)的导函数,由a≤0求得导函数的零点,得到原函数的极值点,从而求得函数F(x)的极小值,也是最小值;
(Ⅲ)由函数F(x)在(0,2)内存在两个极值点,得其导函数在(0,2)上有两个零点,由此得到不等式组
,求解不等式组得答案.
(Ⅱ)求出函数F(x)的导函数,由a≤0求得导函数的零点,得到原函数的极值点,从而求得函数F(x)的极小值,也是最小值;
(Ⅲ)由函数F(x)在(0,2)内存在两个极值点,得其导函数在(0,2)上有两个零点,由此得到不等式组
|
解答:
解:(Ⅰ)g(x)=
+lnx,则g′(x)=-
+
=
,
∴g′(1)=-1,
又g(1)=2,
∴曲线y=g(x)在点(1,g(1))处的切线方程为y-2=-1×(x-1).
即x+y-3=0;
(Ⅱ)F(x)=f(x)-ag(x)=
-a(
+lnx),
F′(x)=
-a(-
+
)=
(x>0).
∵a≤0,
∴当x∈(0,2)时,F′(x)<0,函数F(x)为减函数,在x∈(2,+∞)上F′(x)>0,函数F(x)为增函数.
∴当x=2时,函数有最小值为F(2)=
-a(1+ln2);
(Ⅲ)由(Ⅱ)知,F′(x)=
-a(-
+
)=
,
要使函数F(x)在(0,2)内存在两个极值点,则
方程ex-ax=0在(0,2)上有两个不等式实数根,
令t(x)=ex-ax,
则t′(x)=ex-a,
当a≤0时,t′(x)>0,不满足题意,
当a>0时,由则t′(x)=ex-a=0,得x=lna,
由x→0时,t(x)→1,
∴要使函数t(x)在(0,2)上有两个不同的零点,则
,解得:e<a<
.
∴若函数F(x)在(0,2)内存在两个极值点,则a的取值范围是(e,
).
| 2 |
| x |
| 2 |
| x2 |
| 1 |
| x |
| x-2 |
| x2 |
∴g′(1)=-1,
又g(1)=2,
∴曲线y=g(x)在点(1,g(1))处的切线方程为y-2=-1×(x-1).
即x+y-3=0;
(Ⅱ)F(x)=f(x)-ag(x)=
| ex |
| x2 |
| 2 |
| x |
F′(x)=
| ex•x2-2x•ex |
| x4 |
| 2 |
| x2 |
| 1 |
| x |
| x(x-2)(ex-ax) |
| x4 |
∵a≤0,
∴当x∈(0,2)时,F′(x)<0,函数F(x)为减函数,在x∈(2,+∞)上F′(x)>0,函数F(x)为增函数.
∴当x=2时,函数有最小值为F(2)=
| e2 |
| 4 |
(Ⅲ)由(Ⅱ)知,F′(x)=
| ex•x2-2x•ex |
| x4 |
| 2 |
| x2 |
| 1 |
| x |
| x(x-2)(ex-ax) |
| x4 |
要使函数F(x)在(0,2)内存在两个极值点,则
方程ex-ax=0在(0,2)上有两个不等式实数根,
令t(x)=ex-ax,
则t′(x)=ex-a,
当a≤0时,t′(x)>0,不满足题意,
当a>0时,由则t′(x)=ex-a=0,得x=lna,
由x→0时,t(x)→1,
∴要使函数t(x)在(0,2)上有两个不同的零点,则
|
| e2 |
| 2 |
∴若函数F(x)在(0,2)内存在两个极值点,则a的取值范围是(e,
| e2 |
| 2 |
点评:本题考查了利用导数研究过曲线上某点处的切线方程,考查了利用导数求函数的最值,训练了函数零点的判断方法,考查了数学转化思想方法,是高考试卷中的压轴题.

练习册系列答案
相关题目
已知函数f(x)=sin(ωx+φ)(其中ω>0|φ|<
)图象相邻对称轴的距离为
,一个对称中心为(-
,0),为了得到g(x)=cosωx的图象,则只要将f(x)的图象( )
| π |
| 2 |
| π |
| 2 |
| π |
| 6 |
A、向右平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向左平移
|
数列{an}的通项公式an=n2+2n,则数列{
}的前10项和为( )
| 1 |
| an |
A、
| ||
B、
| ||
C、
| ||
D、
|
 已知函数f(x)=x-
已知函数f(x)=x-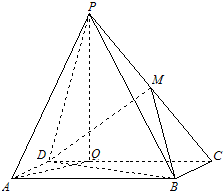 如图,四棱锥P-ABCD中,底面ABCD是矩形,AB=4,AD=2,点P在底面的射影Q在CD上,且PQ=
如图,四棱锥P-ABCD中,底面ABCD是矩形,AB=4,AD=2,点P在底面的射影Q在CD上,且PQ=