Question

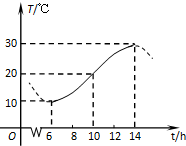如图，某地一天中6时至14时的温度变化曲线近似满足函数y=Asin（ωx+φ）+b（其中ω＞0，

π

2

＜φ＜π），则估计中午12时的温度近似为（　　）

• A、30℃
• B、27℃
• C、25℃
• D、24℃

Answer 1

考点：由y=Asin（ωx+φ）的部分图象确定其解析式

专题：三角函数的图像与性质

分析：由函数的图象的顶点坐标求出A和b，由周期求出ω，由五点法作图求出φ的值，可得函数的解析式，从而其求得x=12时的值．

解答： 解：由函数的图象可得b=20，A=30-20=10，根据

1

4

•

2π

ω

=10-6，可得ω=

π

8

．
再根据五点法作图可得，

π

8

×6+φ=

3π

2

，求得φ=

3π

4

，∴y=10sin（

π

8

x+

3π

4

）+20．
令x=12，可得y=10sin（

3π

2

+

3π

4

）+20=10sin

π

4

+20  10×

2

2

+20≈27℃，
故选：B．

点评：本题主要考查由函数y=Asin（ωx+φ）的部分图象求解析式，属于基础题．