题目内容
下列四个函数中,与y=x表示同一函数的是( )
A、y=
| |||
B、y=
| |||
C、y=(
| |||
D、y=
|
考点:判断两个函数是否为同一函数
专题:函数的性质及应用
分析:根据两个函数的定义域相同,对应关系也相同,这样的两个函数是同一函数,进行判断即可.
解答:
解:对于A,y=
=x(x≠0),与y=x(x∈R)的定义域不同,∴不是同一函数;
对于B,y=
=x(x∈R),与y=x(x∈R)的定义域相同,对应关系也相同,∴是同一函数;
对于C,y=(
)2=x(x≥0),与y=x(x∈R)的定义域不同,∴不是同一函数;
对于D,y=
=|x|(x∈R),与y=x(x∈R)的对应关系不同,∴不是同一函数.
故选:B.
| x2 |
| x |
对于B,y=
| 3 | x3 |
对于C,y=(
| x |
对于D,y=
| x2 |
故选:B.
点评:本题考查了判断两个函数是否为同一函数的问题,解题时应判断它们的定义域是否相同,对应关系是否也相同,是基础题.

练习册系列答案
相关题目
已知向量
=(-2,-6),|
|=
,
•
=10,则向量
与
的夹角为( )
| a |
| b |
| 10 |
| a |
| b |
| a |
| b |
| A、150° | B、-30° |
| C、120° | D、60° |
已知函数f(x)=sin(ωx+φ)(其中ω>0|φ|<
)图象相邻对称轴的距离为
,一个对称中心为(-
,0),为了得到g(x)=cosωx的图象,则只要将f(x)的图象( )
| π |
| 2 |
| π |
| 2 |
| π |
| 6 |
A、向右平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向左平移
|
已知A={y|y=x2-2};B={ y|y=-x2+2},则A∩B=( )
A、{(-
| ||||
B、[-
| ||||
| C、[-2,2] | ||||
D、{-
|
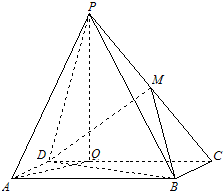 如图,四棱锥P-ABCD中,底面ABCD是矩形,AB=4,AD=2,点P在底面的射影Q在CD上,且PQ=
如图,四棱锥P-ABCD中,底面ABCD是矩形,AB=4,AD=2,点P在底面的射影Q在CD上,且PQ=