题目内容
设集合A={x|10+3x-x2≥0},B={x|m+1≤x≤2m-1},如果有A∩B=B,则实数m的取值范围是( )
| A、(-∞,3] |
| B、[-3,3] |
| C、[2,3] |
| D、[2,5] |
考点:子集与交集、并集运算的转换
专题:集合
分析:解二次不等式可求出集合A,进而分B=∅和B≠∅两种情况分析满足条件A∩B=B的m的取值范围,讨论结果,可得答案.
解答:
解:∵集合A={x|10+3x-x2≥0}={x|-2≤x≤5},
∴当m+1>2m-1,即m<2时,B=∅,满足A∩B=B;
当m+1≤2m-1,即m≥2时,B≠∅,
由A∩B=B得,A?B,
即
解得:-1≤m≤3,
∴2≤m≤3
综上所述实数m的取值范围是(-∞,3].
故选:A.
∴当m+1>2m-1,即m<2时,B=∅,满足A∩B=B;
当m+1≤2m-1,即m≥2时,B≠∅,
由A∩B=B得,A?B,
即
|
解得:-1≤m≤3,
∴2≤m≤3
综上所述实数m的取值范围是(-∞,3].
故选:A.
点评:本题考查的知识点是子集与交集,并集运算的转换,其中要注意B为空集仍满足条件.

练习册系列答案
相关题目
设A,B为两个互不相同的集合,命题p:x∈A∩B,命题q:x∈A或x∈B,则¬q是¬p的( )
| A、充分且必要条件 |
| B、充分非必要条件 |
| C、必要非充分条件 |
| D、非充分且非必要条件 |
下列判断正确的是( )
A、函数f(x)=
| ||
| B、函数f(x)=x2-|x|是偶函数 | ||
| C、函数f(x)=x0是非奇非偶函数 | ||
| D、函数f(x)=2既是奇函数又是偶函数 |
 一个几何体的三视图如图所示,其中正视图是正三角形,则几何体的外接球的表面积为( )
一个几何体的三视图如图所示,其中正视图是正三角形,则几何体的外接球的表面积为( )A、
| ||
B、
| ||
C、
| ||
D、
|
若变量x,y满足
,实数z是2x和-4y的等差中项,则z的最大值等于( )
|
| A、1 | B、2 | C、3 | D、4 |
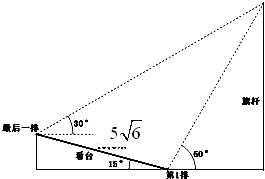 某校运动会开幕式上举行升旗仪式,旗杆正好处在坡度15°的看台的某一列的正前方,从这一列的第一排和最后一排测得旗杆顶部的仰角分别为60°和30°,第一排和最后一排的距离为5
某校运动会开幕式上举行升旗仪式,旗杆正好处在坡度15°的看台的某一列的正前方,从这一列的第一排和最后一排测得旗杆顶部的仰角分别为60°和30°,第一排和最后一排的距离为5