题目内容
设平面向量
=(m,1),
=(2,n),其中m,n∈{1,2,3,4}.记“使得
⊥(
-
)成立的(m,n)”为事件A,则事件A发生的概率为( )
| am |
| bn |
| am |
| am |
| bn |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:古典概型及其概率计算公式
专题:概率与统计
分析:由题意知本题是一个等可能事件的概率,列举出所有的事件,共有16种结果,根据向量垂直的充要条件,列出关于m,n的关系式,根据所给的集合中的元素,列举出所有满足条件的事件,得到概率.
解答:
解:由题意知本题是一个等可能事件的概率,
有序数对(m,n)的所有可能结果是:
(1,1)(1,2)(1,3)(1,4)(2,1)(2,2)(2,3)(2,4)
(3,1)(3,2)(3,3)(3,4)(4,1)(4,2)(4,3)(4,4)共有16个,
满足条件的事件是
⊥(
-
),
∴m2-2m+1-n=0,
∴n=(m-1)2
∵m,n都是集合{1,2,3,4}的元素.
∴事件A包含的基本事件为(2,1)和(3,4),共有2个,
∴所求的概率是P=
=
.
故选C.
有序数对(m,n)的所有可能结果是:
(1,1)(1,2)(1,3)(1,4)(2,1)(2,2)(2,3)(2,4)
(3,1)(3,2)(3,3)(3,4)(4,1)(4,2)(4,3)(4,4)共有16个,
满足条件的事件是
| am |
| am |
| bn |
∴m2-2m+1-n=0,
∴n=(m-1)2
∵m,n都是集合{1,2,3,4}的元素.
∴事件A包含的基本事件为(2,1)和(3,4),共有2个,
∴所求的概率是P=
| 2 |
| 16 |
| 1 |
| 8 |
故选C.
点评:本题考查等可能事件的概率,考查向量垂直的充要条件,本题解题的关键是不重不漏的列举出事件,本题是一个中档题目.

练习册系列答案
相关题目
设集合A={x|10+3x-x2≥0},B={x|m+1≤x≤2m-1},如果有A∩B=B,则实数m的取值范围是( )
| A、(-∞,3] |
| B、[-3,3] |
| C、[2,3] |
| D、[2,5] |
若某程序框图如图所示,则该程序运行后输出的值是( )


| A、4 | B、5 | C、6 | D、7 |
已知实数x,y满足
,则z=x+y的最大值是( )
|
| A、0 | B、2 | C、4 | D、8 |
已知实数a,b满足log
a=log
b,下列五个关系式:
①a>b>1
②0<b<a<1
③b>a>1
④0<a<b<1
⑤a=b
其中不可能成立的关系有( )
| 1 |
| 2 |
| 1 |
| 3 |
①a>b>1
②0<b<a<1
③b>a>1
④0<a<b<1
⑤a=b
其中不可能成立的关系有( )
| A、1 个 |
| B、2 个 |
| C、3 个 |
| D、4个 |
若集合A={x∈R||x+1|+|x-2|≤5},非空集合B={x∈R|2a≤x≤a+3},且B⊆A,则实数a的取值范围是( )
| A、(0,+∞) |
| B、[-1,+∞) |
| C、(-1,0) |
| D、[-1,0] |
某程序框图如图所示,则该程序运行后输出的值是( )


A、
| ||
B、
| ||
C、
| ||
D、
|
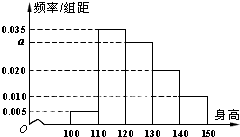 从某小学随机抽取100名同学,将他们的身高(单位:厘米)数据绘制成频率分布直方图(如图).由图中数据可知a=
从某小学随机抽取100名同学,将他们的身高(单位:厘米)数据绘制成频率分布直方图(如图).由图中数据可知a=