题目内容
给定区域D:
,令点集T={(x0,y0)∈D|x0,y0∈Z,(x0,y0)是z=x+y在D上取得最大值或最小值的点},则T中的点共确定 个不同的三角形.
|
考点:简单线性规划
专题:不等式的解法及应用
分析:作出不等式组对应的平面区域,确定z=x+y的最大值或最小值,利用x0,y0∈Z,确定满足条件的点的个数即可得到结论.
解答:
 解:作出目标函数对应的直线,
解:作出目标函数对应的直线,
因为直线z=x+y与直线x+y=4平行和x+y=2平行,
故直线z=x+y过直线x+y=4上的整数点:(4,0),(3,1),(2,2),(1,3)或(0,4)时,直线的纵截距最大,z最大;
故直线z=x+y过直线x+y=2上的整数点:(0,2),(1,1),此时直线的纵截距最小,z最小;
所以满足条件的点共有7个,
则T中的点共确定不同的三角形的个数为
-
=35-10=25,
即T中的点共确定25个不同的三角形.
故答案为:25
 解:作出目标函数对应的直线,
解:作出目标函数对应的直线,因为直线z=x+y与直线x+y=4平行和x+y=2平行,
故直线z=x+y过直线x+y=4上的整数点:(4,0),(3,1),(2,2),(1,3)或(0,4)时,直线的纵截距最大,z最大;
故直线z=x+y过直线x+y=2上的整数点:(0,2),(1,1),此时直线的纵截距最小,z最小;
所以满足条件的点共有7个,
则T中的点共确定不同的三角形的个数为
| C | 3 7 |
| C | 3 5 |
即T中的点共确定25个不同的三角形.
故答案为:25
点评:本题主要考查线性规划的应用,利用数形结合得到这整数点的个数是解决本题的关键,间距使用的排列组合的基础知识.

练习册系列答案
相关题目
设集合A={x|10+3x-x2≥0},B={x|m+1≤x≤2m-1},如果有A∩B=B,则实数m的取值范围是( )
| A、(-∞,3] |
| B、[-3,3] |
| C、[2,3] |
| D、[2,5] |
若集合A={x∈R||x+1|+|x-2|≤5},非空集合B={x∈R|2a≤x≤a+3},且B⊆A,则实数a的取值范围是( )
| A、(0,+∞) |
| B、[-1,+∞) |
| C、(-1,0) |
| D、[-1,0] |
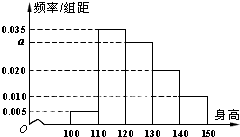 从某小学随机抽取100名同学,将他们的身高(单位:厘米)数据绘制成频率分布直方图(如图).由图中数据可知a=
从某小学随机抽取100名同学,将他们的身高(单位:厘米)数据绘制成频率分布直方图(如图).由图中数据可知a=