题目内容
12.设Sn为正项数列{an}的前n项和,a1=2,Sn+1(Sn+1-2Sn+1)=3Sn(Sn+1),则a100等于( )| A. | 2×398 | B. | 4×398 | C. | 2×399 | D. | 4×399 |
分析 由题意结合因式分解可得(Sn+1-3Sn)(Sn+1+Sn+1)=0,即有Sn+1=3Sn,运用等比数列的通项公式和数列的递推式,即可得到所求值.
解答 解:Sn为正项数列{an}的前n项和,a1=2,Sn+1(Sn+1-2Sn+1)=3Sn(Sn+1),
可得Sn+12-2Sn+1Sn-3Sn2+Sn+1-3Sn=0,
即有(Sn+1-3Sn)(Sn+1+Sn)+(Sn+1-3Sn)=0,
即为(Sn+1-3Sn)(Sn+1+Sn+1)=0,
即有Sn+1=3Sn,
数列{Sn}为等比数列,首项为2,公比为3,
可得Sn=2×3n-1,
则a100=S100-S99=2×399-2×398
=4×398.
故选:B.
点评 本题考查数列的递推式的运用,考查等比数列的通项公式的运用,考查变形及化简整理的运算能力,属于中档题.

练习册系列答案
 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
2.如图所示是一个组合几何体的三视图,则该几何体的体积为( )
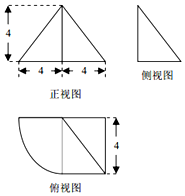

| A. | $\frac{16}{3}$π | B. | $\frac{64}{3}$ | C. | $\frac{16π+64}{3}$ | D. | 16π+64 |
3.计算2sin275°-1的值等于( )
| A. | $\frac{1}{2}$ | B. | $-\frac{1}{2}$ | C. | $-\frac{{\sqrt{3}}}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
7.在公比为2的等比数列{an}中,a1a3=6a2,则a4等于( )
| A. | 4 | B. | 8 | C. | 12 | D. | 24 |
17.若复数z=3-2i,则z的共轭复数$\overline{z}$( )
| A. | -3+2i | B. | -3-2i | C. | -2+3i | D. | 3+2i |
4.计算:sin72°cos18°+cos72°sin18°=( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | 1 | D. | -1 |
1.设等差数列{an}的前n项和为Sn,若a1=-11,a4+a6=-6,则a3等于( )
| A. | 16 | B. | 37 | C. | -7 | D. | 9 |