题目内容
4.计算:sin72°cos18°+cos72°sin18°=( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | 1 | D. | -1 |
分析 根据正弦的和与差公式直接求解.
解答 解:sin72°cos18°+cos72°sin18°=sin(72°+18°)=sin90°=1.
故选C.
点评 本题主要考查正弦的和与差公式的计算.比较基础

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
12.设Sn为正项数列{an}的前n项和,a1=2,Sn+1(Sn+1-2Sn+1)=3Sn(Sn+1),则a100等于( )
| A. | 2×398 | B. | 4×398 | C. | 2×399 | D. | 4×399 |
9.定义“规范03数列”{an}如下:{an}共有2m项,其中m项为0,m项为3,且对任意k≤2m,a1,a2,…,ak中0的个数不少于3的个数,若m=4,则不同的“规范03数列”共有( )
| A. | 18个 | B. | 16个 | C. | 14个 | D. | 12个 |
13.已知抛物线x2=2py上的点M(m,3)到它的焦点的距离为5,则该抛物线的准线方程为( )
| A. | y=-2 | B. | y=2 | C. | x=-2 | D. | x=2 |
14.曲线f(x)=x2+2x+ex在点(0,f(0))处的切线的方程为( )
| A. | y=x-1 | B. | y=x+1 | C. | y=3x-1 | D. | y=3x+1 |
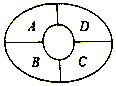 如图某综艺节目现场设有A,B,C,D四个观众席,现有由5不同颜色的马甲可供现场观众选择,同一观众席上的马甲的颜色相同,相邻观众席上的马甲的颜色不相同,则不同的安排方法种数为260.
如图某综艺节目现场设有A,B,C,D四个观众席,现有由5不同颜色的马甲可供现场观众选择,同一观众席上的马甲的颜色相同,相邻观众席上的马甲的颜色不相同,则不同的安排方法种数为260.