题目内容
1.设函数f(x)=cos(2x-$\frac{4π}{3}$)+2cos2x.(1)求f(x)的最大值,并写出使f(x)取得最大值时x的集合;
(2)求f(x)的单调递增区间;
(3)已知△ABC中,角A,B,C的对边分别为a,b,c,若f(B+C)=$\frac{3}{2}$,b+c=2,求a的最小值.
分析 (1)由三角函数公式化简可得f(x)=cos(2x+$\frac{π}{3}$)+1,由三角函数的最值可得;
(2)解2kπ+π≤2x+$\frac{π}{3}$≤2kπ+2π可得单调递增区间;
(3)由(2)和f(B+C)=$\frac{3}{2}$可得角A=$\frac{π}{3}$,由余弦定理和基本不等式可得.
解答 解:(1)由三角函数公式化简可得
f(x)=cos(2x-$\frac{4π}{3}$)+2cos2x
=cos2xcos$\frac{4π}{3}$+sin2xsin$\frac{4π}{3}$+2cos2x
=-$\frac{1}{2}$cos2x-$\frac{\sqrt{3}}{2}$sin2x+1+cos2x
=$\frac{1}{2}$cos2x-$\frac{\sqrt{3}}{2}$sin2x+1
=cos(2x+$\frac{π}{3}$)+1,
当2x+$\frac{π}{3}$=2kπ即x=kπ-$\frac{π}{6}$(k∈Z)时,f(x)取得最大值2,
此时x的集合为{x|x=kπ-$\frac{π}{6}$,k∈Z};
(2)由2kπ+π≤2x+$\frac{π}{3}$≤2kπ+2π可解得kπ+$\frac{π}{3}$≤x≤kπ+$\frac{5π}{6}$,
∴f(x)的单调递增区间为[得kπ+$\frac{π}{3}$,kπ+$\frac{5π}{6}$],k∈Z;
(3)由(2)可得f(B+C)=cos(2B+2C+$\frac{π}{3}$)+1=$\frac{3}{2}$,
∴cos(2B+2C+$\frac{π}{3}$)=$\frac{1}{2}$,由角的范围可得2B+2C+$\frac{π}{3}$=$\frac{5π}{3}$,
变形可得B+C=$\frac{2π}{3}$,A=$\frac{π}{3}$,
由余弦定理可得a2=b2+c2-2bccosA=b2+c2-bc
=(b+c)2-3bc=4-3bc≥4-3($\frac{b+c}{2}$)2=1
当且仅当b=c=1时取等号,故a的最小值为1
点评 本题考查三角函数恒等变换,涉及正余弦定理和基本不等式,属中档题.

 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案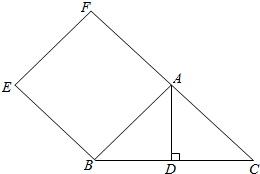 如图,已知正方形ABEF的面积为10,以AB为直角边所作的等腰直角角形ABC的斜边BC=2$\sqrt{5}$,求BC边上的高AD的长度.
如图,已知正方形ABEF的面积为10,以AB为直角边所作的等腰直角角形ABC的斜边BC=2$\sqrt{5}$,求BC边上的高AD的长度.