题目内容
设z1=i4+i5+i6+…+i12，z2=i4•i5•i6•…•i12，则z1，z2的关系是（ ）
| A、z1=z2 |
| B、z1=-z2 |
| C、z1=1+z2 |
| D、无法确定 |
考点：复数代数形式的混合运算
专题：数系的扩充和复数
分析：由等比数列的求和公式化简，然后利用虚数单位i的运算性质计算z1，利用指数的运算性质结合虚数单位i的运算性质求解z2，则答案可求．
解答：
解：∵z1=i4+i5+i6…+i12=
=
=1，
z2=i4•i5•i6…i12=i4+5+6+…+12=i
=i72=（i4）18=1．
∴z1=z2．
故选：A．
| i4(1-i9) |
| 1-i |
| 1-i |
| 1-i |
z2=i4•i5•i6…i12=i4+5+6+…+12=i
| (4+12)×9 |
| 2 |
∴z1=z2．
故选：A．
点评：本题考查了复数代数形式的混合运算，考查虚数单位i的运算性质，是基础题．
练习册系列答案
相关题目
设α，β都是锐角，且sinα=
，sinβ=
，则α+β=（ ）
| ||
| 10 |
| ||
| 5 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
函数y=log
（-x2+2x+3）的单调递减区间为（ ）
| 1 |
| 2 |
| A、（0，+∞） |
| B、（-1，3） |
| C、（-1，1] |
| D、[1，3） |
已知复数z满足z=
（i为虚数单位），则复数z所对应的点所在象限为（ ）
| 3+i |
| 1+i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
给出下列四个函数图象和函数的四个关系式：
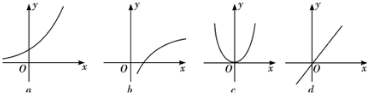
①f（x+y）=f（x）+f（y）；
②g（x+y）=g（x）•g（y）；
③u（x•y）=u（x）+u（y）；
④v（x•y）=v（x）•v（y），已知每个函数图象都有满足其中的一个关系式，则它们之间的对应是（ ）
①f（x+y）=f（x）+f（y）；
②g（x+y）=g（x）•g（y）；
③u（x•y）=u（x）+u（y）；
④v（x•y）=v（x）•v（y），已知每个函数图象都有满足其中的一个关系式，则它们之间的对应是（ ）
| A、①→a ②→d ③→c ④→b |
| B、①→b ②→c ③→a ④→d |
| C、①→c ②→a ③→b ④→d |
| D、①→d ②→a ③→b ④→c |
i是虚数单位，复数z=i-1，则|z|=（ ）
| A、1 | ||
B、
| ||
| C、2 | ||
D、
|
若复数（1+i）（1+ai）（a∈R，i是虚数单位）是纯虚数，则a=（ ）
| A、1 | B、-1 | C、0 | D、2 |
已知全集U=R，集合A={x|
＜0}，B={y|y=2x，x≥0}，则集合{x|x≤0}=（ ）
| x-1 |
| x |
| A、A∩B |
| B、A∪B |
| C、CU（A∩B） |
| D、CU（A∪B） |