题目内容
给出下列四个函数图象和函数的四个关系式:
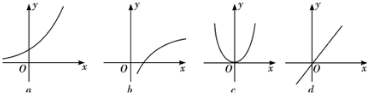
①f(x+y)=f(x)+f(y);
②g(x+y)=g(x)•g(y);
③u(x•y)=u(x)+u(y);
④v(x•y)=v(x)•v(y),已知每个函数图象都有满足其中的一个关系式,则它们之间的对应是( )

①f(x+y)=f(x)+f(y);
②g(x+y)=g(x)•g(y);
③u(x•y)=u(x)+u(y);
④v(x•y)=v(x)•v(y),已知每个函数图象都有满足其中的一个关系式,则它们之间的对应是( )
| A、①→a ②→d ③→c ④→b |
| B、①→b ②→c ③→a ④→d |
| C、①→c ②→a ③→b ④→d |
| D、①→d ②→a ③→b ④→c |
考点:对数函数的图像与性质,函数的图象
专题:函数的性质及应用
分析:①中,用函数y=x模拟,得出函数图象的特征;
②中,用函数y=2x模拟,得出函数图象的特征;
③中,用函数y=lgx模拟,得出函数图象的特征;
④中,用y=x2模拟,得出函数图象的特征.
②中,用函数y=2x模拟,得出函数图象的特征;
③中,用函数y=lgx模拟,得出函数图象的特征;
④中,用y=x2模拟,得出函数图象的特征.
解答:
解:对于①,f(x+y)=f(x)+f(y),是线性函数,可以用函数y=x模拟,函数图象应是d;
对于②,g(x+y)=g(x)•g(y),是指数函数类型的,可以用函数y=2x模拟,图象应是a;
对于③,u(x•y)=u(x)+u(y),是对数函数类型的,可以用函数 y=lgx模拟,图象应是b;
对于④,v(x•y)=v(x)•v(y),是绝对值类型的函数,可以用y=x2模拟,图象应是c.
故选:D.
对于②,g(x+y)=g(x)•g(y),是指数函数类型的,可以用函数y=2x模拟,图象应是a;
对于③,u(x•y)=u(x)+u(y),是对数函数类型的,可以用函数 y=lgx模拟,图象应是b;
对于④,v(x•y)=v(x)•v(y),是绝对值类型的函数,可以用y=x2模拟,图象应是c.
故选:D.
点评:本题考查了函数的图象问题,解答时应观察图象、分析图象、判定图象是表示哪种类型的函数,常见的基本初等函数性质的是什么,是易错题.

练习册系列答案
相关题目
用秦九韶算法求多项式f(x)=7x6+6x4+3x2+2当x=4时的值时,先算的是( )
| A、4×4=16 |
| B、4×4×4×4×4×4=4096 |
| C、7×4+6=34 |
| D、7×4+0=28 |
质点的运动方程是S=
,则质点在t=2时的加速度为( )
| 1 |
| t |
A、
| ||
B、
| ||
C、
| ||
D、
|
一个等比数列共有3m项,其中前m项和为x,中间m项和为y,后m项和为z,则一定有( )
| A、x+y=z |
| B、x+z=2y |
| C、xy=z |
| D、xz=y2 |
在数列{an}中,它的前n项和为Sn=an2+bn+3a-2(n∈N*,其中a,b是常数),若数列{an}是等差数列,则它的公差是( )
A、
| ||
| B、1 | ||
C、
| ||
| D、与a有关 |
设z1=i4+i5+i6+…+i12,z2=i4•i5•i6•…•i12,则z1,z2的关系是( )
| A、z1=z2 |
| B、z1=-z2 |
| C、z1=1+z2 |
| D、无法确定 |
将4名实习教师分配到高一年级三个班实习,每班至少安排一名教师,则不同的分配方案有( )种.
| A、12 | B、36 | C、72 | D、108 |
a=cos50°cos127°+cos40°cos37°,b=
(sin56°-cos56°),c=
,d=
(cos80°-2cos250°+1),则a,b,c,d的大小关系为( )
| ||
| 2 |
| 1-tan239° |
| 1+tan239° |
| 1 |
| 2 |
| A、a>b>d>c |
| B、b>a>d>c |
| C、a>c>b>d |
| D、c>a>b>d |